Распределение Рэлея

Распределение Рэлея введено Дж. У. Рэлеем (1880) в связи с задачей сложения гармонических колебаний со спиральными фазами. Закон Рэлея применяется для описания неотрицательных величин, в частности, когда случайная величина является радиусом - вектором при двухмерном гауссовом распределении. В ткацком производстве закон Рэлея широко применяется для анализа геометрической формы, например некруглости, нецилиндричности, эксцентриситета намотки на сновальных валах и ткацких навоях. Также встречается в применениях теории вероятностей, например к радиотехнике.

Распределение является геометрической суммой случайных величин 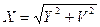, подчиненных закону Гаусса с параметрами: .

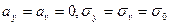Плотность вероятности распределения Рэлея имеет вид:

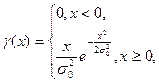(2.3.1)

где 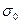- среднее квадратическое отклонение исходного двухмерного распределения 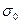 = ). Значение 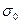является параметром закона Рэлея.

Максимальное значение плотности равно 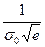и достигается при (на рис.2.3.1 даны графики плотности распределения Рэлея при различных ).

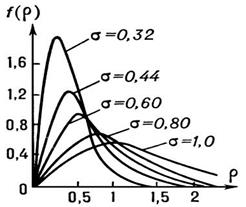
Рис.2.3.1 графики плотности распределения Рэлея при различных

Функция распределения имеет вид: 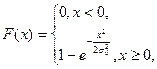(2.3.2)

При замене 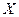новой переменной получим плотность вероятности и функцию распределения нормированного закона Рэлея:

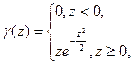(2.3.3)

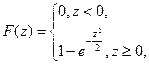(2.3.4)

Графики нормированной плотности вероятности и функции распределения показаны на рис. 2.3.2.

Дифференциальная кривая (рис. 2.3.2,а) имеет положительную асимметрию и более острую вершину, чем гауссово распределение.

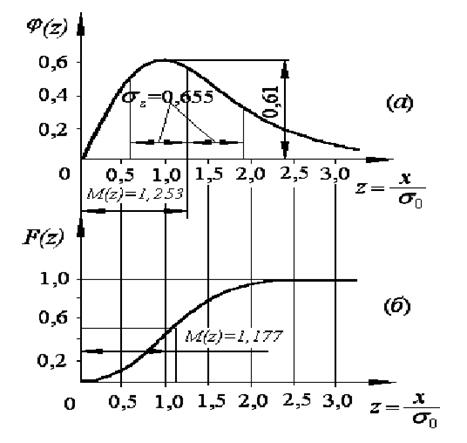
Рис.2.3.2. Плотность вероятности (а) и функция распределения (б) нормированного закона Рэлея.

Вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение:

1. Математическое ожидание.

Следовательно, 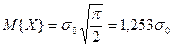(2.3.5)

2.Дисперсия.

.

.

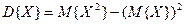
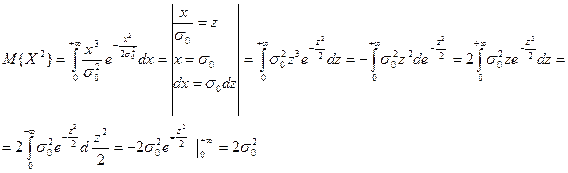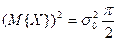Следовательно,

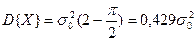(2.3.6)

3.Среднее квадратическое отклонение.

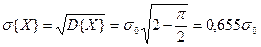(2.3.7).

Вычислим асимметрию и эксцесс:

1.Ассиметрия.

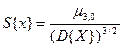_, где .

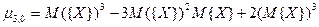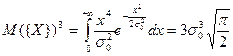
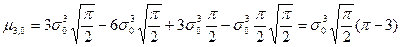
Следовательно,

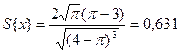(2.3.8)

2.Эксцесс.

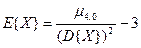_, где .

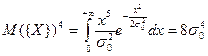
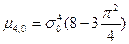
Следовательно,

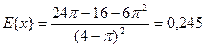(2.3.9)

Нормированное рэлеевское распределение не зависит от параметра 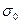и легко табулируется.

Пример

На сновальной машине в результате погрешности крепления в пинолях сновального вала его намотка имеет эксцентриситет. Экспериментально получено, что и минимальный радиус намотки при вращении вала изменяется случайно со средним квадратическим отклонением 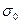=0,5 мм.

Нормированное распределение Рэлея не зависит от параметра 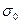, изменение показано на рис. 2.3.1(а), а величины 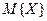и для данного эксперимента 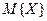=1,25; 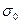=0,63 мм; =0,655; 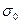=0,33 мм.

Список литературы

1. Орлов А.И. Математика случая. Вероятность и статистика – основные факты. - Учебное пособие. М.: МЗ-Пресс, 2004.

2. http://www.aup.ru/books/m155/

3. Смирнов Н.В., Дунин - Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1965. 511с.

4. Элементы математической статистики/ О.И. Тескин, Н.Е. Козлов, Г.М. Цветкова, Е.М. Пашовкин. М.: Изд-во МГТУ, 1995. 107 с.

5. Бочаров А.А.Теория вероятностей. Математическая статистика. М.: Гардарика, 1998. 328.

6. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: Высш.шк., 1992. 304.

7. Письменный Д. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. М.: Айрис-пресс,2006. 288с.