 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Распределения Пирсона (хи – квадрат), Стьюдента и Фишера
|
|
В приложениях статистики очень часто используют связанные с нормальным распределения: распределение  (хи-квадрат), распределение Стьюдента (часто применяют обозначение t-распределение) и F-распределение. Плотности этих распределений выражаются через стандартные математические функции в виде некоторых (довольно громоздких) формул, которые и служат определением распределений. Мы же дадим «конструктивное» определение, раскрывающее возможности использования этих распределений в математической статистике. Рассматриваемые распределения в настоящее время часто используются при статистической обработке данных.
(хи-квадрат), распределение Стьюдента (часто применяют обозначение t-распределение) и F-распределение. Плотности этих распределений выражаются через стандартные математические функции в виде некоторых (довольно громоздких) формул, которые и служат определением распределений. Мы же дадим «конструктивное» определение, раскрывающее возможности использования этих распределений в математической статистике. Рассматриваемые распределения в настоящее время часто используются при статистической обработке данных.
Распределение Пирсона  (хи - квадрат) – распределение случайной величины
(хи - квадрат) – распределение случайной величины  , где случайные величины
, где случайные величины  независимы и имеют одно и тоже распределение
независимы и имеют одно и тоже распределение  . При этом число слагаемых, т.е.
. При этом число слагаемых, т.е.  , называется «числом степеней свободы» распределения хи – квадрат.
, называется «числом степеней свободы» распределения хи – квадрат.
Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных. График функции плотности распределения  изображен на рис. 2.1.1 в двух вариантах:
изображен на рис. 2.1.1 в двух вариантах: 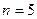 и
и  .
.

Рис. 2.1.1. Функция плотности  -распределения: (1) n=5, (2) n=10.
-распределения: (1) n=5, (2) n=10.
Основные характеристики  - распределения
- распределения
| Обозначение | 
|
| Область значений | 
|
| Параметры |  – параметр формы, целое положительное число; его часто называют числом степеней свободы. – параметр формы, целое положительное число; его часто называют числом степеней свободы.
|
| Плотность (функция вероятности) | 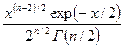 , где , где  – гамма-функция – гамма-функция
|
| Математическое ожидание | 
|
| Дисперсия | 
|
| Функция распределения | Не выражается в элементарных функциях |
| Медиана | ~ 
|
| Мода |  , если , если 
|
| Коэффициент асимметрии | 
|
| Коэффициент эксцесса | 
|
Свойства распределения.
1. Распределение  устойчиво относительно суммирования. Если
устойчиво относительно суммирования. Если  - независимы, и
- независимы, и  , то
, то  .
.
2. В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины  может быть приближено нормальным
может быть приближено нормальным  . Более точно
. Более точно  при
при  .
.
Связь с другими распределениями 
1. 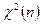 совпадает с гамма – распределением:
совпадает с гамма – распределением:  . Это соотношение позволяет вычислять функцию распределения хи-квадрат.
. Это соотношение позволяет вычислять функцию распределения хи-квадрат.
2. Если  и
и  – независимые случайные величины, то случайная величина
– независимые случайные величины, то случайная величина  имеет распределение Фишера со степенями свободы (
имеет распределение Фишера со степенями свободы ( ).
).
3. Если случайная величина  имеет F-распределение с
имеет F-распределение с  и
и  степенями свободы, то случайная величина
степенями свободы, то случайная величина  распределена как хи-квадрат с
распределена как хи-квадрат с  степенями свободы.
степенями свободы.
4. Если случайная величина  подчиняется
подчиняется  - распределению Стьюдента с
- распределению Стьюдента с  степенями свободы, а
степенями свободы, а  – стандартному нормальному распределению, причем
– стандартному нормальному распределению, причем  и
и  независимы, то случайная величина
независимы, то случайная величина  распределена как хи-квадрат с
распределена как хи-квадрат с  степенями свободы.
степенями свободы.
5. Если  независимые нормальные случайные величины, т.е.
независимые нормальные случайные величины, т.е.  ,
, 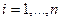 , то случайная величина
, то случайная величина  имеет распределение хи-квадрат с
имеет распределение хи-квадрат с  степенями свободы.
степенями свободы.
Дата публикования: 2014-11-18; Прочитано: 4112 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
