 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример распределения хи-квадрат
|
|
Пусть фирма выпустила новый процессор. Предположим, что каждые два года цена на этот процессор падает на 10%. Тогда количество таких процессоров, которые можно купить на фиксированную сумму может быть описано с помощью распределения хи-квадрат.
Доказательство:
Обозначим фиксированную сумму через Z. Пусть S - стартовая цена процессора. Тогда по прошествии  лет он будет стоить
лет он будет стоить  . Преобразуем полученное выражение:
. Преобразуем полученное выражение:  . Введем новую переменную:
. Введем новую переменную:  . Получим следующую формулу:
. Получим следующую формулу:  . Количество процессоров, которые можно купить на фиксированную сумму, равно
. Количество процессоров, которые можно купить на фиксированную сумму, равно 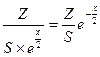 . Если закрыть глаза на коэффициенты, то полученная формула соответствует формуле плотности для распределения хи-квадрат при
. Если закрыть глаза на коэффициенты, то полученная формула соответствует формуле плотности для распределения хи-квадрат при  .
.
Распределение  Стьюдента – это распределение случайной величины
Стьюдента – это распределение случайной величины  ,
,
где случайные величины  и
и 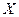 независимы,
независимы,  имеет стандартное нормальное распределение
имеет стандартное нормальное распределение  , а
, а 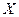 – распределение хи – квадрат с
– распределение хи – квадрат с  степенями свободы. При этом
степенями свободы. При этом  называется «числом степеней свободы» распределения Стьюдента.
называется «числом степеней свободы» распределения Стьюдента.
Распределение Стьюдента было введено в 1908 г. английским статистиком В.Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В.Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В.Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.
В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.
В теории вероятностей дается следующее конструктивное определение распределения Стьюдента.
Предположим, что каждая из  независимых случайных величин
независимых случайных величин 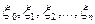 , распределена нормально с параметрами
, распределена нормально с параметрами  и
и 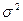 (
( ). Тогда случайная величина
). Тогда случайная величина  имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенями свободы (записывается
степенями свободы (записывается  ).
).
График функции плотности  -распределения см. на рис. 2.1.2 в двух вариантах:
-распределения см. на рис. 2.1.2 в двух вариантах:  и
и  . Заметим, что максимальное значение плотности распределения достигается при
. Заметим, что максимальное значение плотности распределения достигается при  , и график симметричен относительно оси ординат.
, и график симметричен относительно оси ординат.

Рис. 2.1.2. Функция плотности  -распределения в двух вариантах: (1)
-распределения в двух вариантах: (1)  , (2)
, (2)  .
.
Основные характеристики распределения Стьюдента
| Обозначение | 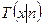
|
| Область значений | 
|
| Параметры | Параметр формы  , число степеней свободы, целое положительное число , число степеней свободы, целое положительное число
|
| Плотность (функция вероятности) | 
|
| Математическое ожидание | 
|
| Дисперсия |  , если , если 
|
| Функция распределения | Не выражается в элементарных функциях |
| Медиана | 
|
| Мода | 
|
| Коэффициент асимметрии |  , если , если 
|
| Коэффициент эксцесса |  , где , где 
|
Свойства распределения.
1. Распределение Стьюдента симметрично. В частности, если  , то
, то  .
.
2. Случайная величина  имеет только моменты порядков
имеет только моменты порядков 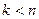 , причем
, причем 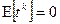 , если
, если  - нечетно;
- нечетно;  , если
, если  - четно. Моменты порядков
- четно. Моменты порядков 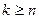 не определены.
не определены.
Связь с другими распределениями:
1. Распределение Стьюдента сходится к стандартному нормальному при  . Пусть дана последовательность случайных величин
. Пусть дана последовательность случайных величин  , где
, где  ,
,  . Тогда
. Тогда 
 по распределению при
по распределению при  .
.
2. Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть  , тогда
, тогда 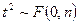 .
.

Дата публикования: 2014-11-18; Прочитано: 2581 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
