Векторное произведение, свойства

Даны три вектора 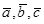с общим началом и не лежащие в од-ной плоскости.

Определение 18. Тройка векторов 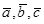называется правой (левой) тройкой, если кратчайший поворот от 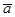к 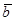виден из конца вектора происходящим против (по) часовой стрелки.

Рис.25

Если в тройке поменять местами какие-то два вектора, а третий оставить на своем месте, то тройка изменит свою “ориентацию”. Например, если 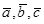- правая тройка, то - левая тройка. При циклической перестановке векторов в тройке “ориентация” тройки не меняется. Например, если 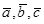- правая тройка, то - тоже правая тройка.

Смысл декартовой тройки должен соответствовать вы-бранному правилу.

Рис.26

На рисунке 26 первая тройка – правая, а вторая тройка – левая.

Определение 19. Векторным произведением двух векторов 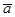и 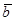называется вектор , удовлетворяющий следующим услови-

ям:

1. он перпендикулярен векторам 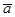и 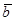, то есть перпендикуля-рен плоскости векторов 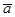и ;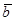

2. длина этого вектора равна площади параллелограмма, постро-енного на векторах 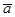и 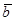, то есть ;

3. тройка 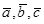- правая.

Обозначения или .