Доказательство. 3. Доказательство.а) Для очевидно;

Рис.27

3. Доказательство. а) Для очевидно;

б) для : если длина одной из сторон параллелограмма изменяется в раз, то площадь параллелограмма тоже изме-нится в раз;

в) для : .

4. .

Доказательство. Возьмем единичный вектор , перпендику-лярный плоскости 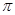, . Спроектируем вектор 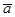на плоскость 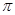, получим вектор , повернем его в плоскости 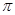вокруг точки по часовой стрелке на :

а) ;

Рис.28

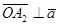б) (так как , (так как , а - проекция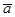

тогда по теореме о трех перпендикулярах выполняется этот факт);

в) - правая тройка, следовательно, .

Рис.29

Вектор . В . Спроектируем данный треугольник на плоскость 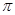, получим , повернем его в плоскости 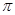по часовой стрелке на , получим . .

Так как , то .

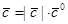, тогда , следовательно, .

5. .

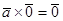6. Для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нулю.

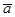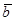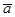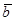Доказательство. а) Пусть векторы и коллинеарны, следо-вательно, или , тогда и , нулевую длину имеет только нулевой вектор, то есть ;б) пусть , тогда , но , следовательно, , а это значит, что и коллинеарны.

7. .

8. Векторные произведения базисных ортов можно представить в виде таблицы:

			-

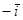
Пояснение: векторное произведение - это вектор, перпендикулярный векторам и , длина которого равна площади квадрата, построенного на векторах и , то есть равна 1, а тройка векторов - правая тройка, отсюда следует, что . Остальные произведения

можно получить, используя свойства векторного произведения.

Рис.30