Лiнiї другого порядку

Лiнiєю другого порядку, розташованою на площинi xОy, називається всяка лiнiя, координати точок якої задовольняють алгебраїчному рiвнянню другого степеня вiдносно x та y.

Коло. Колом називають множину всiх точок площини 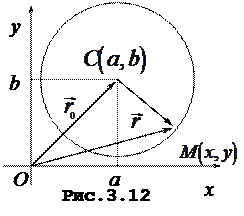xОy, рiвновiддалених вiд заданої точки 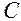, що називається центром, на вiдстань 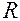- радiус кола. Нехай вiдомi координати цетра кола 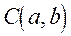i нехай 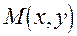- до-вiльна точка кола, 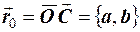- радiус-вектор центра, 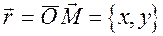- радiус-вектор точки 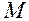. За означенням 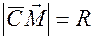, але 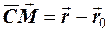, тому 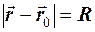векторне рiв-няння кола. В декартових координатах це рiвняння таке:

.

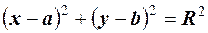Якщо центр 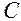кола спiвпадає з початком координат, тобто 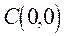, то рiвняння кола має простий вигляд

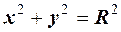
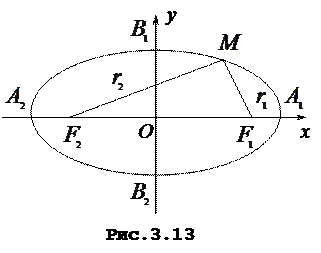Елiпс. Елiпсом називають множину всiх точок 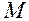площини xОy, сума вiдстаней яких до двох заданих точок 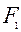та 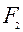, що називаються фокусами, є величина стала, рiвна 2a (рис. 3.13).

Виведемо найпростiше рiвняння елiпса, вибравши систему координат таким способом: вiсь Оx побудуємо на прямiй, що з¢єднує точки 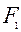i 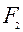. Через середину вiдрiзка 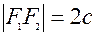, проведемо вiсь Оy. У вибранiй системi координат фокуси мають координати , .

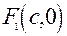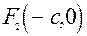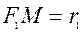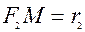Вiдрiзки i називаються фокальними радi-усами елiпса. За означенням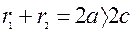 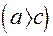. Нехай 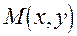- довiльна точка елiпса. Тодi

; .

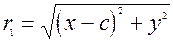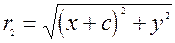Рiвняння елiпса приймає вигляд

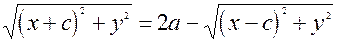
Пiднесемо обидвi частини цього рiвняння до квадрата

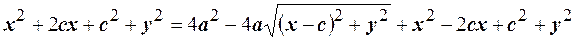
або 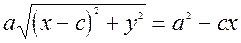; ще раз пiднесемо до квадрата

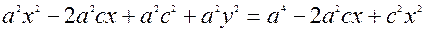
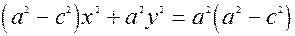; позначимо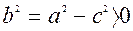

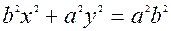. Роздiлимо обидвi частини на ,

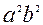. Це канонiчне рiвняння елiпса.

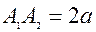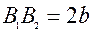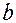Тут - велика вiсь елiпса, - мала вiсь, вiдповiдно - велика пiввiсь, - мала пiввiсь. Ексцентриситетом елiпса називають число .

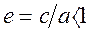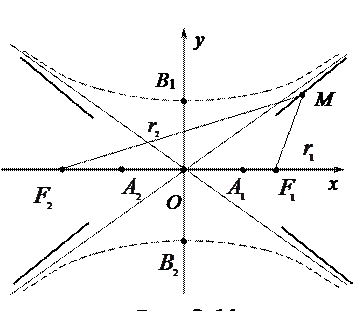
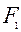Гiпербола. Гiперболою називають множину всiх точок площини xОy, рiзниця вiддалей яких до двох заданих точок та 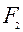, що нази-ваються фокусами, є ве-личина постiйна, рiвна 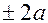. (ця величина повинна бути меншою за вiддаль ).

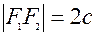Виведемо найпростiше рiвняння гiперболи, вибравши систему координат як у випадку елiпса. У вибранiй системi координат фокуси мають координати , .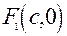

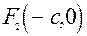Нехай 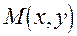- довiльна точка гiперболи. Тодi фо-кальнi радiуси гiперболи

, .

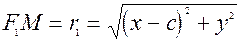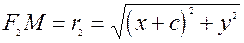За означенням гiперболи 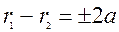. Пiдставимо сюди вирази для фокальних радiусiв, одержимо рiвняння

.

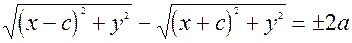Пiсля елементарних перетворень отримаємо канонiчне рiв-няння гiперболи

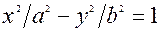, (18*)

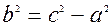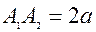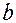де . При цьому - дiйсна вiсь гiпер-боли, - дiйсна пiввiсь, - уявна пiввiсь (рис. 3.14).

Ексцентриситетом гiперболи називають число .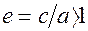

Прямi 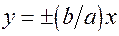називаються асимптотами гiперболи (#).

Гiпербола, що задана рiвнянням 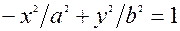, називається спряженою гiперболi (18*). На рис. 3.14 вона зображена пунктирною лiнiєю. У спряженої гiперболи асимптоти тi ж. Гiпербола з рiвними пiввiсями 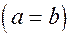називається рiвносторонньою, її асимптоти спiвпадають з бiсектрисами координатних кутiв.

(#) Пряма 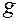називається асимптотою лiнiї 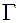, якщо вiдстань мiж точками прямоє 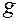i лiнiї 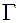прямує до нуля, коли точка вiддаляється в нескiнченнiсть.

Парабола. Параболою називається множина всiх точок 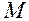площини xОy,однаково вiддалених вiд заданої точки ,

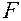що називається фокусом, та вiд за-даної прямої d, що називається ди-ректрисою (пряма d не проходить че-рез точку F). Виведемо найпростiше рiвняння параболи, вибравши систему координат таким чином: вiсь Оx проведемо через точку F перпендику-лярно директрисi d (рис. 3.15), через середину вiдрiзка TF (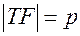, p - параметр параболи)проведемо вiсь Оy.

У вибранiй системi координат фокус F має координати . Нехай 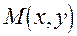- довiльна точка параболи.

Позначимо вiддаль , 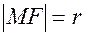. За означенням параболи r=d. Виразимо r i d через координати точок

,

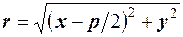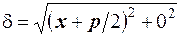
Таким чином, одержали рiвняння:

.

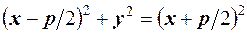Пiднесемо обидвi частини цього рiвняння до квадрата

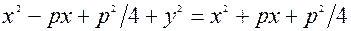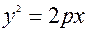або (19*)

Рiвняння (19*) називають канонiчним рiвнянням пара-боли, p - параметр параболи, причому p>0. Ця парабола симетрична вiдносно вiсi Оx, проходить через початок координат, вiтки параболи направленi уздовж вiсi Оx. У параболи 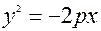вiтки направленi проти вici Оx. Рiв-няння 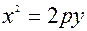також визначає параболу, що проходить че-рез початок координат, симетричну вiдносно вici Оy, при p>0 вiтки параболи направленi наверх, у параболи 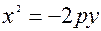вiтки направленi вниз.

У парабол 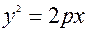та 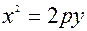вiccю симетрiї явля-ється та вiсь, що входить в рiвняння в першiй степенi.