 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Остроградского-Гаусса в векторной форме
|
|
Пусть поверхность 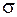 - замкнутая, ограничивающая тело
- замкнутая, ограничивающая тело  , объем которого обозначим через
, объем которого обозначим через  .
.
В этом случае 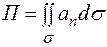 называется обильностью поля
называется обильностью поля  в теле
в теле  .
.
Если 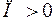 , то говорят, что в теле
, то говорят, что в теле  есть источники; если
есть источники; если 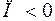 - то стоки поля
- то стоки поля  .
.
Тогда отношение
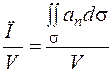
можно рассматривать как среднюю плотность источников и стоков, распределенных в теле  .
.
Зафиксируем теперь внутри поверхности 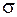 некоторую точку
некоторую точку  . Обозначим через
. Обозначим через  диаметр области
диаметр области  и будем стягивать поверхность
и будем стягивать поверхность 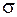 к точке
к точке  , устремляя
, устремляя  к нулю. Если при этом существует конечный предел указанного отношения, то он называется дивергенцией поля
к нулю. Если при этом существует конечный предел указанного отношения, то он называется дивергенцией поля 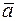 в точке
в точке  и обозначается так:
и обозначается так: 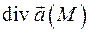 или
или 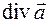 , т.е.
, т.е.
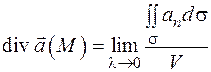 .
.
Можно доказать, что, если координаты  вектора
вектора 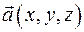 непрерывны в области
непрерывны в области  и имеют непрерывные частные производные
и имеют непрерывные частные производные 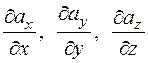 , то для любой точки
, то для любой точки  области
области  дивергенция существует и может быть вычислена по формуле
дивергенция существует и может быть вычислена по формуле
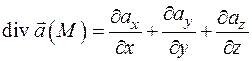 . (2.13)
. (2.13)
Обратимся теперь к формуле Остроградского-Гаусса. Положив в ней 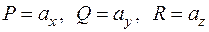 , можем написать
, можем написать
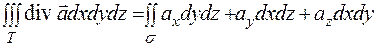 .
.
Далее воспользуемся формулой перехода от поверхностного интеграла второго рода к интегралу первого рода. Тогда
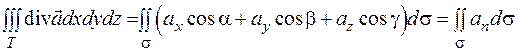 .
.
Таким образом, теорему Остроградского-Гаусса можно сформулировать в векторной форме.
Поток векторного поля  через замкнутую поверхность
через замкнутую поверхность 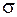 в сторону внешней нормали равен тройному интегралу от дивергенции этого поля по телу
в сторону внешней нормали равен тройному интегралу от дивергенции этого поля по телу  , ограниченному поверхностью
, ограниченному поверхностью 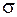 , т.е.
, т.е.
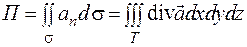 . (2.14)
. (2.14)
Пример 2.8. Найти с помощью теоремы Остроградского-Гаусса поток векторного поля 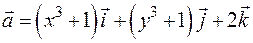 через поверхность тела, ограниченного конусом
через поверхность тела, ограниченного конусом 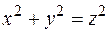 и плоскостью
и плоскостью 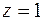 .
.
Решение. Вычислим дивергенцию поля  , используя формулу (2.13):
, используя формулу (2.13):
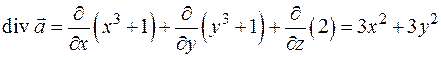 .
.
В соответствии с формулой (2.14) имеем
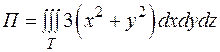 .
.
Вычислим тройной интеграл, переходя к цилиндрическим координатам:
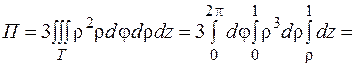
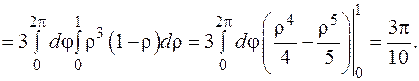
Дата публикования: 2014-11-19; Прочитано: 4277 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
