Решение задач. Задача 2.1.Найти линии уровня для плоского скалярного поля

Задача 2.1. Найти линии уровня для плоского скалярного поля .

Решение. В соответствии с формулой (2.1) линии уровня определяются уравнением 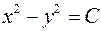. Это семейство гипербол при 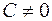и две прямые (при ).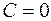

Задача 2.2. Найти поверхности уровня для пространственного скалярного поля .

Решение. В соответствии с формулой (2.2) поверхности уровня определяются уравнением или 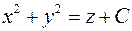. Эти уравнения определяют семейство эллиптических параболоидов с вершинами на оси 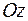в точках .

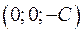Задача 2.3. Найти производную скалярного поля 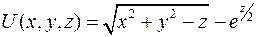в точке 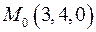по направлению вектора .

Решение. Найдем сначала единичный вектор 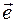, задающий направление вектора .

.

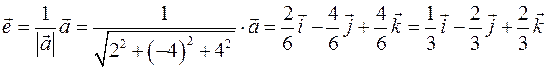Значит, . Теперь вычислим частные производные функции в точке .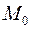

Тогда в соответствии с формулой (2.4) имеем

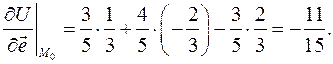
Задача 2.4. Найти градиент скалярного поля 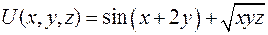: а) в произвольной точке 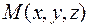; б) в точке .

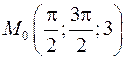Решение. Вычислим частные производные функции .

;

;

.

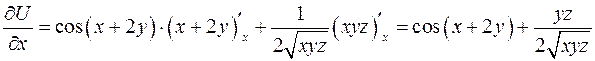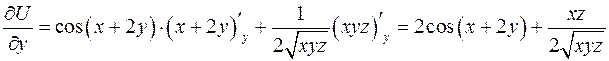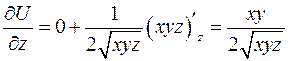Тогда по формуле (2.5) получаем в производной точке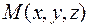

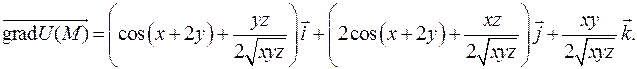
Для нахождения градиента в точке 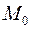подставим вместо координаты точки :

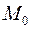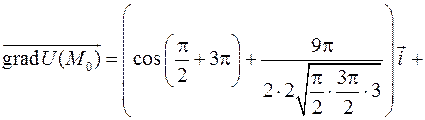
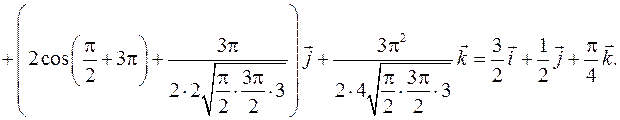Задача 2.5. Проверить, будет ли скалярное поле 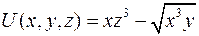гармоническим.

Решение. Вычислим частные производные функции сначала первого, и потом второго порядка.

;

.

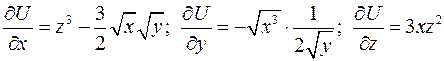Тогда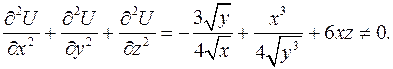

Значит, поле не будет гармоническим.

Вопросы для самопроверки по теме 2.1

1. Дайте определение скалярного поля.

2. Дайте определение линии уровня и поверхности уровня.

3. Дайте определение производной по направлению.

4. Напишите формулу для вычисления производной по направлению.

5. Что такое градиент скалярного поля?

6. Какое скалярное поле называется гармоническим?