 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение потока векторного поля
|
|
Потоком  векторного поля
векторного поля  через двустороннюю поверхность
через двустороннюю поверхность 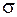 в выбранную сторону называется поверхностный интеграл
в выбранную сторону называется поверхностный интеграл
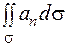 , (2.9)
, (2.9)
где 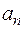 - проекция поля
- проекция поля  на единичнуюнормаль к поверхности
на единичнуюнормаль к поверхности  , направление которой соответствует выбранной стороне поверхности, т.е.
, направление которой соответствует выбранной стороне поверхности, т.е.  .
.
Так как 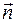 - нормаль единичная, то
- нормаль единичная, то 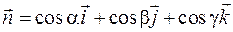 , где
, где  - углы, образованные вектором
- углы, образованные вектором 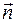 с осями
с осями  соответственно. Тогда
соответственно. Тогда  , и, следовательно,
, и, следовательно,
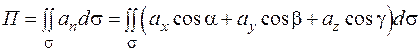 . (2.10)
. (2.10)
Если поверхность 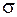 задается уравнением
задается уравнением 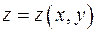 , то направляющие косинусы нормали вычисляются по формулам
, то направляющие косинусы нормали вычисляются по формулам
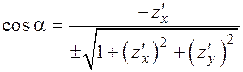 ,
, 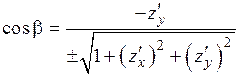 ,
,
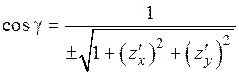 . (2.11)
. (2.11)
Знаки перед радикалами выбираются так, чтобы направление нормали соответствовало выбранной стороне поверхности.
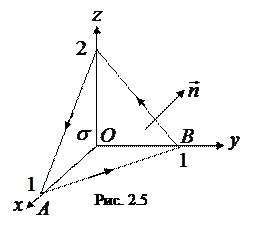 Пример 2.7. Вычислить поток векторного поля
Пример 2.7. Вычислить поток векторного поля 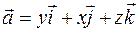 через часть плоскости
через часть плоскости 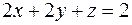 , лежащую в первом октанте, в направлении нормали, образующей острый угол с осью
, лежащую в первом октанте, в направлении нормали, образующей острый угол с осью 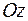 (рис. 2.5).
(рис. 2.5).
Решение. Спроектируем поверхность 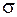 на плоскость
на плоскость  и перейдем в интеграле (2.10) от поверхностного к двойному. При этом
и перейдем в интеграле (2.10) от поверхностного к двойному. При этом 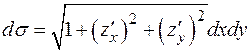 , а направляющие косинусы заменяем по формулам (2.11), причем перед радикалами выбираем знак "+", так как в условии задачи сказано, что
, а направляющие косинусы заменяем по формулам (2.11), причем перед радикалами выбираем знак "+", так как в условии задачи сказано, что 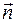 образует с осью
образует с осью 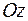 острый угол и, значит,
острый угол и, значит, 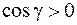 . Таким образом,
. Таким образом,
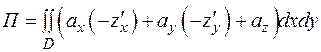 , (2.12)
, (2.12)
где 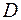 - проекция
- проекция 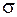 на плоскость
на плоскость  , т.е. треугольник
, т.е. треугольник 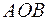 ;
; 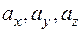 - координаты векторного поля
- координаты векторного поля  , причем переменная
, причем переменная  заменена на
заменена на 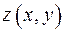 из уравнения поверхности, т.е.
из уравнения поверхности, т.е. 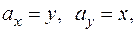
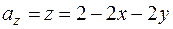 .
.
Выразим из уравнения плоскости  и вычислим
и вычислим 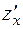 и
и 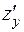 :
: 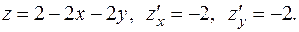
Подставляя в формулу (2.12), получаем
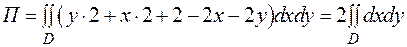 .
.
Последний интеграл представляет собой площадь треугольника 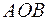 и, следовательно,
и, следовательно,
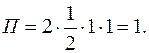
Дата публикования: 2014-11-19; Прочитано: 1091 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
