 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Градиент скалярного поля
|
|
Определение. Градиентом скалярного поля  в точке
в точке 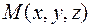 называется вектор, координатами которого являются частные производные
называется вектор, координатами которого являются частные производные  функции
функции 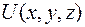 в этой точке.
в этой точке.
Обозначается градиент символом 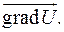 Итак,
Итак,
 (2.5)
(2.5)
В плоском скалярном поле  вектор
вектор  определяется равенством
определяется равенством
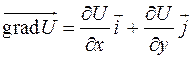 .
.
Пример 2.4. Дано скалярное поле 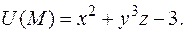 Найти градиент поля в точке
Найти градиент поля в точке 
Решение. Находим частные производные

Вычисляем их значения в точке 

Записав формулу (2.5) в виде  ,
,
имеем 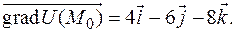
Дата публикования: 2014-11-19; Прочитано: 778 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
