 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Потенциальное векторное поле
|
|
Векторное поле  называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле  , для которого
, для которого  служит градиентом, т.е.
служит градиентом, т.е.
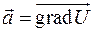 .
.
Напомним, что это равенство означает, что
 . (2.20)
. (2.20)
Это скалярное поле  называется потенциалом (потенциальной функцией, скалярным потенциалом) поля
называется потенциалом (потенциальной функцией, скалярным потенциалом) поля  . Примерами потенциальных полей могут служить электрическое поле точечного заряда, поле тяготения, магнитное поле, созданное прямолинейным проводником, по которому течет постоянный электрический ток.
. Примерами потенциальных полей могут служить электрическое поле точечного заряда, поле тяготения, магнитное поле, созданное прямолинейным проводником, по которому течет постоянный электрический ток.
Необходимое и достаточное условие потенциальности векторного поля:
чтобы поле  было потенциальным, необходимо и достаточно, чтобы в каждой точке ротор
было потенциальным, необходимо и достаточно, чтобы в каждой точке ротор  равнялся нулю, т.е.
равнялся нулю, т.е.
 (2.21)
(2.21)
Поэтому потенциальное векторное поле называют также безвихревым.
Основные свойства потенциального поля:
1. Циркуляция потенциального поля по любому кусочно-гладкому замкнутому контуру равна нулю.
2. Линейный интеграл от потенциального поля по кусочно-гладкому пути не зависит от пути.
Потенциал поля  можно найти по формулам
можно найти по формулам
 (2.22)
(2.22)
или
 (2.23)
(2.23)
где  - некоторая фиксированная точка в рассматриваемой области,
- некоторая фиксированная точка в рассматриваемой области,  - произвольная постоянная.
- произвольная постоянная.
Пример 2.11. Показать, что поле 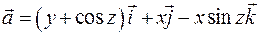 потенциально во всем пространстве и найти его потенциал.
потенциально во всем пространстве и найти его потенциал.
Решение. Вычислим  , используя формулу (2.19):
, используя формулу (2.19):
 ,
,
т.е. поле  потенциально во всем пространстве. Для нахождения потенциала воспользуемся формулой (2.23), а в качестве точки
потенциально во всем пространстве. Для нахождения потенциала воспользуемся формулой (2.23), а в качестве точки  возьмем начало координат.
возьмем начало координат.

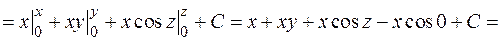

Дата публикования: 2014-11-19; Прочитано: 6771 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
