Гармоническое поле

Если скалярное поле удовлетворяет уравнению

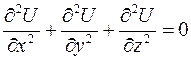, (2.6)

то это поле называется гармоническим.

Плоское поле 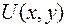будет гармоническим, если оно удовлетворяет уравнению .

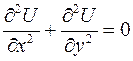Пример 2.5. Проверить, является ли скалярное поле 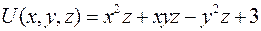гармоническим.

Решение. Вычислим частные производные, входящие в уравнение (2.6).

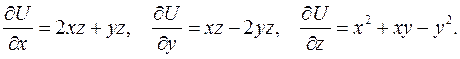
Тогда

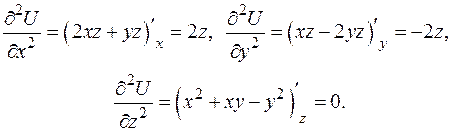
Следовательно,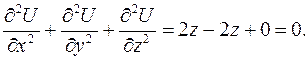

Значит, поле удовлетворяет уравнению (2.6), т.е. является гармоническим.