 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Производная по направлению
|
|
Производная по направлению
Важной характеристикой скалярного поля является величина, показывающая, как быстро меняется поле в данном направлении.
Пусть задано скалярное поле 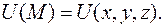 Возьмем точку
Возьмем точку  и единичный вектор
и единичный вектор  (координаты единичного вектора равны его направляющим косинусам). На линии действия вектора в направлении этого вектора возьмем точку
(координаты единичного вектора равны его направляющим косинусам). На линии действия вектора в направлении этого вектора возьмем точку 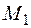 .
.
Если при стремлении точки 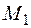 к точке
к точке  так, что точка
так, что точка 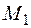 остается на линии действия вектора
остается на линии действия вектора 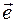 , существует конечный предел отношения
, существует конечный предел отношения  то этот предел называется производной скалярного поля
то этот предел называется производной скалярного поля 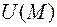 или функции
или функции 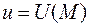 в точке
в точке  по направлению вектора
по направлению вектора 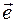 и обозначается
и обозначается 
Итак,
 (2.3)
(2.3)
Производную по направлению можно вычислить по формуле:
 (2.4)
(2.4)
Производная по направлению в плоском скалярном поле  также вычисляется по формуле (2.4), в которой надо положить
также вычисляется по формуле (2.4), в которой надо положить  то есть отбросить последнее слагаемое.
то есть отбросить последнее слагаемое.
 Пример 2.3. Найти производную функции
Пример 2.3. Найти производную функции  в точке
в точке 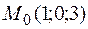 в направлении вектора
в направлении вектора  если
если 
Решение. Найдем сначала единичный вектор 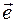 , задающий направление, по которому надо определить производную. Для этого находим вектор
, задающий направление, по которому надо определить производную. Для этого находим вектор  или
или 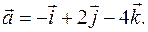
Тогда
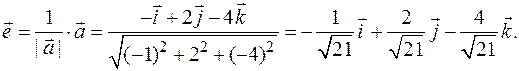
Отсюда
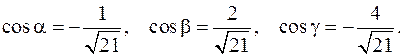
Далее находим частные производные функции 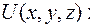

Вычисляем значения их в точке 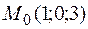

Записав формулу (2.4) в виде
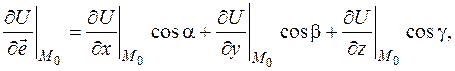
имеем
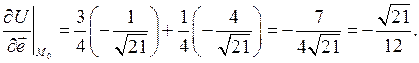
Дата публикования: 2014-11-19; Прочитано: 835 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
