 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. Задачу решим МПС матричным способом
|
|
Задачу решим МПС матричным способом. В этом случае целесообразно использовать программируемую вычислительную технику. Решим задачу в среде MathCAD.
1. Назначаем в качестве переменных состояния ток в индуктивности и напряжение на конденсаторе – i 3 (t) и uC(t). Выходная переменная – ток i 1 (t).
2. Независимые начальные условия нулевые:
i 3 ( 0+ ) = i 3 ( 0- ) = 0, uC( 0+ ) = uC( 0- ) = 0.
3. Составим систему уравнений состояния, используя законы Кирхгофа:
L 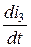 = uL = uC – r 2× i 3; i 1 =
= uL = uC – r 2× i 3; i 1 = 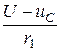 ; С
; С 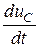 = i 2 = i 1 – i 3 =
= i 2 = i 1 – i 3 = 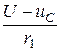 – i 3.
– i 3.
Таким образом, система уравнений состояния имеет вид:
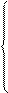
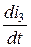 = -
= - 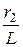 i 3 +
i 3 + 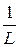 uC,
uC,
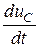 = -
= - 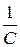 i 3 –
i 3 – 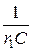 uC +
uC + 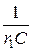 u.
u.
Эта же система в матричном виде: 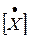 = [ K ] ´ [ X ] + [ L ] ´ [ F ]. (*)
= [ K ] ´ [ X ] + [ L ] ´ [ F ]. (*)
Итак, матрица переменных состояния [ X ], матрица коэффициентов [ K ], столбцовая матрица свободных членов [ L ] ´ [ F ] и матрица независимых начальных условий [ X (0) ] имеют вид:
[ X ] =  , [ K ] =
, [ K ] = 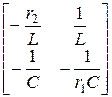 , [ L ] ´ [ F ] =
, [ L ] ´ [ F ] =  , [ X (0) ] =
, [ X (0) ] = 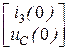 =
= 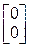 .
.
Решение системы уравнений состояния:
X (t) = e K t · Ф (t), где Ф (t) = 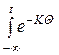 · L ´ F (q) · dq, то есть
· L ´ F (q) · dq, то есть
X (t) = e K t 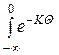 · L ´ F (q) · dq + e K t
· L ´ F (q) · dq + e K t 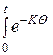 · L ´ F (q) · dq =
· L ´ F (q) · dq =
= e K t · X ( 0 ) + e K t 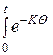 · L ´ F (q) · dq. (**)
· L ´ F (q) · dq. (**)
4. Получим матричную экспоненциальную функцию e K t.
Сначала определим собственные значения l матрицы [ K ], то есть корни уравнения det( [ K ] – l · 1) = 0, где 1 = Е – единичная матрица порядка K:
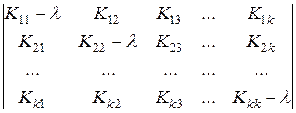 = 0.
= 0.
В данном случае характеристическое уравнение: 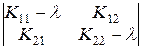 = 0.
= 0.
При двух корнях характеристического уравнения матричная экспонента находится в виде e K t = a 0 Е + a 1 [ K ],
где коэффициенты ai находят из следующей системы уравнений:
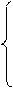 a 0 + l 1 a 1 = el 1· t , a 0 =
a 0 + l 1 a 1 = el 1· t , a 0 = 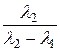 el 1· t +
el 1· t + 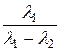 el 2· t ,
el 2· t ,
a 0 + l 2 a 1 = el 2· t . a 1 = 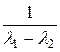 el 1· t +
el 1· t + 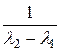 el 2· t .
el 2· t .
5. Далее переменные состояния можно найти по формуле (**), а выходную переменную i 1 (t) по формуле i 1 = 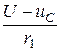 .
.
6. Ниже приводится программа расчётов в среде MathCAD с построенными графиками i 1 (t) и i 3 (t).
j:= 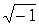 ORIGIN:= 1 U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4
ORIGIN:= 1 U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4
E:= 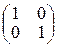 x0:=
x0:= 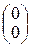 K:=
K:= 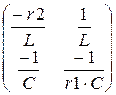 LF(q):=
LF(q):= 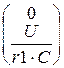
|K - l·E| 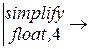 .1667e6 + 566.7·l + l2
.1667e6 + 566.7·l + l2
|K - l·E| = 0 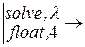
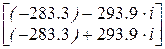
Перезадание корней характеристического уравнения l:= 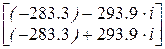
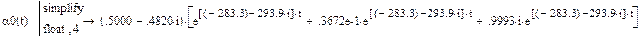 |
a0(t):=
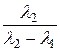 ·
· 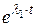 +
+ 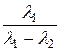 ·
· 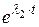 a1(t):=
a1(t):= 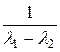 ·
· 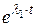 +
+ 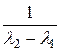 ·
· 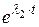
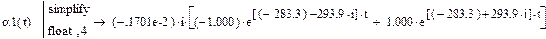 |
eK(t):= a0(t)·E + a1(t)·K i3(t):= (eK(t)·x0)1 +
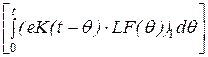
uC(t):= (eK(t)·x0)2 + 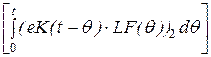 i1(t):=
i1(t):= 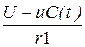
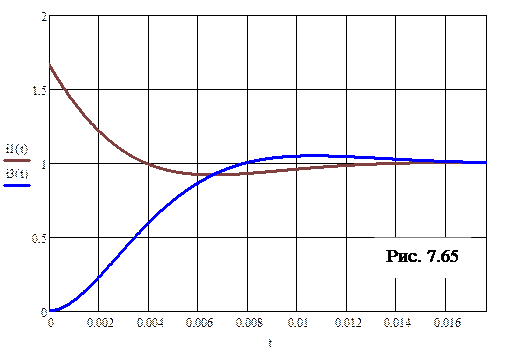 |
 Примечание. Ответы для коэффициентов a 0, a 1, искомых токов i 1 (t) и i 3 (t) (то же наблюдается и в отношении матричной экспоненты e K t) содержат комплексные числа. Это объясняется комплексностью корней характеристического уравнения. Однако, благодаря тому, что корни являются комплексными сопряжёнными числами, значения указанных величин в любой момент времени оказываются действительными, в связи с чем возможно построение графиков токов. Приведение же ответов для токов к стандартному виду с затухающей синусоидой требует дополнительных действий. В этом состоит недостаток данного метода. Графики искомых токов показаны на рис. 7.65.
Примечание. Ответы для коэффициентов a 0, a 1, искомых токов i 1 (t) и i 3 (t) (то же наблюдается и в отношении матричной экспоненты e K t) содержат комплексные числа. Это объясняется комплексностью корней характеристического уравнения. Однако, благодаря тому, что корни являются комплексными сопряжёнными числами, значения указанных величин в любой момент времени оказываются действительными, в связи с чем возможно построение графиков токов. Приведение же ответов для токов к стандартному виду с затухающей синусоидой требует дополнительных действий. В этом состоит недостаток данного метода. Графики искомых токов показаны на рис. 7.65. 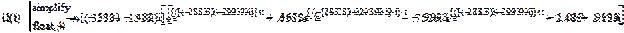 |
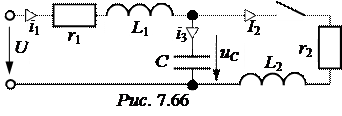
ЗАДАЧА 7.44. Построить график напряжения на конденса-торе uC(t) схемы рис. 7.66, при условии r 1 = 60 Ом, L 1= 0,2 Гн, r 2 = 40 Ом, L 2= 0,1 Гн, C = 100 мкФ, u = 100 В.
Комментарии и ответы.
Задачу 7.44 решим по той же самой методике, что и задачу 7.43.
Исходные данные: j:= 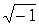 ORIGIN:= 1
ORIGIN:= 1
U:= 100 r1:= 60 r2:= 40 L:= 0.1 C:= 10-4
Переменные состояния: i 1, i 2, uC. Независимые начальные условия:
i 1 ( 0+ ) = i 1 ( 0- ) = 0, i 2 ( 0+ ) = i 2 ( 0- ) = 0, uC( 0+ ) = uC( 0- ) = u = 100 В x0:= 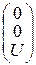
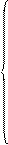 Система уравнений состояния:
Система уравнений состояния: 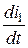 = -
= - 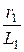 i 1 –
i 1 – 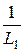 uC +
uC + 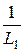 u,
u,
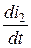 = -
= - 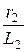 i 2 +
i 2 + 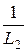 uC,
uC,
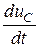 =
= 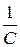 i 1 –
i 1 – 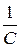 i 2.
i 2.
E:= 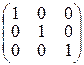 K:=
K:= 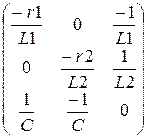 LF(q):=
LF(q):= 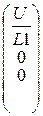
|K - l·E| 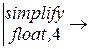 (-.2700e6)·l – 700·l2 –.5000е8 – 1.·l3
(-.2700e6)·l – 700·l2 –.5000е8 – 1.·l3
|K - l·E| = 0 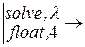
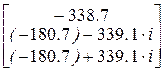
Перезадание корней характеристического уравнения l:= 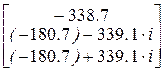
Коэффициенты ai находят из следующей системы уравнений:
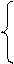 a 0 + l 1 a 1 + l 12 a 2 = el 1· t,
a 0 + l 1 a 1 + l 12 a 2 = el 1· t,
a 0 + l 2 a 1 + l 22 a 2 = el 2· t,
a 0 + l 3 a 1 + l 32 a 2 = el 3· t.
D:= 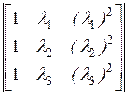
a0(t):= 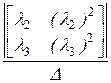 ·
· 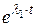 +
+ 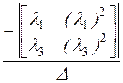 ·
· 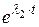 +
+ 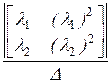 ·
· 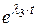
a1(t):= 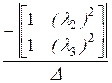 ·
· 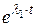 +
+ 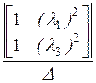 ·
· 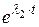 +
+ 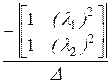 ·
· 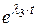
a2(t):= 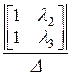 ·
· 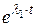 +
+ 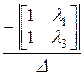 ·
· 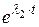 +
+ 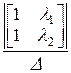 ·
· 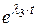
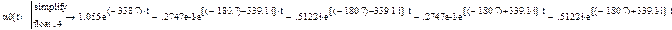 Ответ, например, для коэффициента a0(t):
Ответ, например, для коэффициента a0(t):
В случае трёх корней характеристического уравнения матричная экспонента находится в виде e K t = a 0 Е + a 1 [ K ] + a 2 [ K ] 2,
eK(t):= a0(t)·E + a1(t)·K + a2(t)·K2
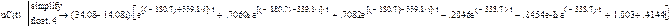
uC(t):= (eK(t)·x0)3 + 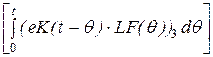
Попробуем получить ответ для uC(t):
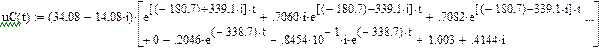 |
По данной формуле MathCAD отказывается давать значения напряже-ния в отдельные моменты времени. Поэтому произведём перезадание uC(t):
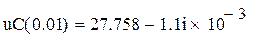 |
Значение напряжения, например, в момент времени t = 0,01 с:
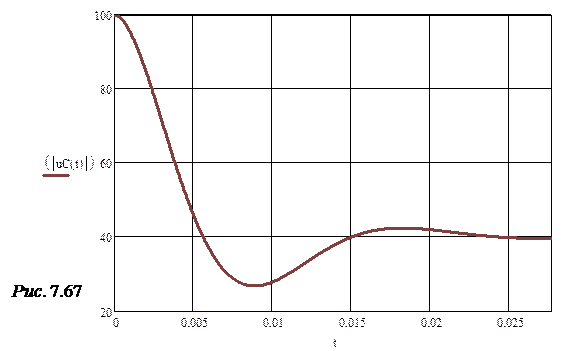 |
Примечание. Как и в задаче 7.43 значения a 0, a 1, e K t и, конечно же, uC должны быть в любой момент времени действительными числами. Здесь же значение uC (0,01) оказалось комплексным. Это объясняется тем, что при перезадании корней характеристического уравнения li было сделано округление ответов до четырёх значащих цифр, что внесло в последующие вычисления некоторую погрешность. Например, у значений напряжения на конденсаторе появилась мнимая часть. Однако она мала и ей можно пренебречь. Можно утверждать, что реальное значение напряжения на конденсаторе практически равно модулю от полученного комплексного значения. В связи с этим строим график модуля напряжения uC в функции времени t (рис.7.67).
Дата публикования: 2014-11-19; Прочитано: 308 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
