Решение. Расчётная схема установки приведена на рис

Расчётная схема установки приведена на рис. 7.37,а, периодическая последовательность импульсов u(t) – на рис. 7.37,б, на котором указаны но-мера n (начиная с момента подключения нагрузки) действующих импульсов. Период следования импульсов Т = f ^-1 =0,02 с, продолжительность действия импульса t ₀ = ½ Т =0,01 с, продолжительность паузы t_П = ½ Т =0,01 с.

Ниже мы рассмотрим несколько способов расчёта установившейся реакции, но для всех их требуется расчёт переходного процесса в электрической цепи при действии первого импульса. Этот расчёт можно произвести любым методом расчёта переходных процессов (классическим методом, операторным методом, с помощью интеграла Дюамеля).

Для интервала действия первого импульса t( 0 … t ₀ ) рис. 7.37,б и u(t) = U_msinwt

i = I_msin(wt – j) + I_msinj · e ^{– t / t},

где I_m = 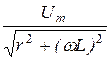= = 4,94 A,

j = arctg 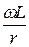= arctg = 85,45°,

постоянная времени цепи t = L / r = 0,2/5 = 0,04 с,

отношение t / Т = 0,04/0,02 = 2 или t = 2 Т.

Численный результат расчёта i = 4,94 sin( 314 t – 85,45° ) + 4,92· e ^{–25 t} A.

В момент t = t ₀ = ½ Т действие импульса заканчивается, а ток достигает значения i(t ₀ ) = 4,94 sin( 180° – 85,45° ) + 4,92· e ^–25·0,01= 8,75 А.

В момент времени t ₀ диод VD рис. 7.36 запирается, а нулевой диод VD ₀ отпирается, ток обмотки возбуждения продолжает протекать по цепи r - L - VD ₀, для которой уравнение состояния определяется вторым законом Кирхгофа ir + L = 0.

Решение этого уравне-ния для t > t ₀

i = A 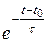= 8,75· 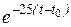A

(постоянная интегрирования А определена на основании первого закона коммутации i(t _0- ) = i(t ₀₊ ) = 8,75 А).

По окончании паузы t = T = 0,2 c, i(T) = 6,81 A. Кривая тока в период действия первого импульса приведена на рис. 7.38.

1. Способ расчёта установившейся реакции методом неопределённых начальных условий.

Анализируя переход-ный процесс при действии первого импульса напряже-ния, замечаем, что к началу следующего импульса (а значит, и каждого из по-следующих импульсов) ток цепи i(T) ≠ 0, i( 2 T) ≠ 0 и т.д.

Для расчёта устано-вившейся реакции перене-сём начало отсчёта времени к моменту поступления (n +1 ) -го импульса при n ® ¥, заменив t ¢ на t. Начальное значение тока на этом интервале не определено: i( 0₊ ) ≠ 0.

Как и при действии первого импульса ток переходного процесса на интервале t( 0 … t ₀ ) i = I_msin(wt – j) + A · e ^{– t / t}, а при t = 0₊ i = i( 0₊ ),тогда

i( 0₊ ) = - I_msinj + A,

откуда постоянная интегрирования A = i( 0₊ ) + I_msinj, а закон изменения тока в пределах действия импульса i = I_msin(wt – j) + [i( 0₊ ) + I_msinj] · e ^{– t / t}.

К моменту окончания действия импульса ток приобретает величину

i(t ₀ ) = I_msin(wt ₀ – j) + [i( 0₊ ) + I_msinj] · .

Так как при t = t ₀ ток в индуктивности не может измениться скачком, то в период паузы i(t) = i(t ₀ ) · 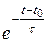, а в конце периода i(T) = i(t ₀ ) · = i( 0 ),

т.е. при периодическом процессе i(T) = i( 0 ).

В развёрнутом виде получаем выражение, из которого и определяется принятое ранее неопределённое начальное значение:

· = i( 0 ),

откуда i( 0 ) = .

Для рассматриваемого численного примера

i( 0 ) = = 17,32 A.

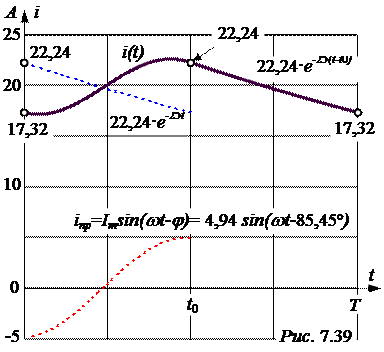
Искомое периодическое решение принимает вид:

i =

кривая периодического решения приведена на рис. 7.39.

2. Способ расчёта установившейся реакции путём наложения реакций в области вещественной переменной t. Рассчитав ПП в электрической цепи на интервале действия первого импульса, используя принцип наложения, рассчитаем реакцию на (n +1 ) -м интервале. При этом учтём, что реакции на каждый отдельный импульс одинаковы, но следуют с запаздыванием во времени, что в полученных ранее выражениях (для первого импульса) приводит к дополнительному при t слагаемому ( - nT).

Результат расчёта ПП в период действия (n +1 ) -го импульса nT £ t £ nT + t ₀

i(t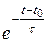) = A + A + A + … + A +

+ I_msin(wt – wnT – j) + I_msinj · .

В период паузы (n +1 ) -го импульса nT + t ₀ £ t £ (n +1 )T

i(t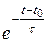) = A + A + A +…+ A .

В приведенных выражениях с экспонентами вынесем общий множитель A 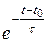. Остальные слагаемые образуют геометрическую прогрессию со знаменателем q = .

Частичные суммы прогрессии 1 + + + … + = ,

1 + + + … + + = .

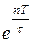В результате в период действия (n +1 ) -го импульса nT £ t £ nT + t ₀

i(t) = A 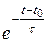+ I_msin(wt – wnT – j) + I_msinj · .

В период паузы на (n +1 ) -м интервале nT + t ₀ £ t £ (n +1 )T

i(t) = A .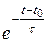

Для практического выполнения расчёта тока на (n +1 ) -м импульсе удобно перенести начало отсчёта времени t ¢ (рис. 7.37,б) в точку начала действия (n +1 ) -го импульса.

Тогда t = nT + t ¢ и t ¢ = t – nT, = = · ,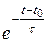

sin(wt – wnT – j) = sin(wt ¢+ wnT – wnT – j) = sin(wt ¢– j).

i(t ¢ ) = A + I_msin(wt ¢– j) + I_msinj · для nT £ t £ nT + t ₀,

i(t ¢ ) = A для nT + t ₀ £ t £ (n +1 )T.

Для расчёта установившейся реакции необходимо устремить n ® ¥ и положить t ¢= t, то есть принять начало отсчёта времени в т. 0¢.

Получим для 0 £ t £ t ₀ i_УСТ(t) = 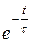+ I_msin(wt – j) + I_msinj · ,

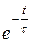для t ₀ £ t £ T i_УСТ(t) = .

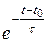Для рассматриваемого примера получаем

для 0 £ t £ t ₀ i_УСТ(t) = + 4,94 sin(wt – j) + 4,92· =

= 4,94 sin( 314 t – 85,45° ) + 22,24· е ^{–25 t} A,

для t ₀ £ t £ T i_УСТ(t) = 22,24· е ^{–25 (t – t 0 )} A,

что совпадает с ранее полученными результатами по методу неопределённых начальных условий.

Решение задачи операторным методом выполнено в ЗАДАЧЕ 7.57.