 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. Уравнение по второму закону Кирхгофа для вторичного контура
|
|
Токи до коммутации:
i 2 (t – )= 0, i 1 (t – )= 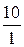 = 10 А.
= 10 А.
Уравнение по второму закону Кирхгофа для вторичного контура
- M 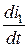 + r × i 2 + L 2
+ r × i 2 + L 2 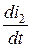 = 0.
= 0.
Ввиду скачкообразного изменения первичного тока с 10 А до 0 производные 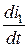 и
и 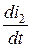 в момент коммутации достигнут бесконечных значений, по сравнению с которыми величиной r × i 2 можно пренебречь. Таким образом, получаем равенство Mdi 1 = L 2 di 2, которое проинтегрируем за время коммутации от t = 0– до t = 0+. За это время токи изменятся:
в момент коммутации достигнут бесконечных значений, по сравнению с которыми величиной r × i 2 можно пренебречь. Таким образом, получаем равенство Mdi 1 = L 2 di 2, которое проинтегрируем за время коммутации от t = 0– до t = 0+. За это время токи изменятся:
i 1 – от i 1 ( 0– ) = 10 А до i 1 ( 0+ ) = 0,
i 2 – от i 2 ( 0– ) = 0 до искомого i 2 ( 0+ ).
L 2 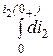 = M
= M 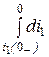 или L 2 i 2 ( 0+ ) = - Mi 1 ( 0– ) = -0,05×10 = -0,5 Вб.
или L 2 i 2 ( 0+ ) = - Mi 1 ( 0– ) = -0,05×10 = -0,5 Вб.
Отсюда i 2 ( 0+ ) = - 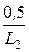 = -
= - 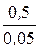 = -10 А.
= -10 А.
Постоянная времени цепи t = 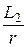 =
= 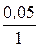 = 0,05 с.
= 0,05 с.
Корень характеристического уравнения р = - t -1= -20 с -1.
Ток переходного процесса i 2 (t) = i 2 ( 0 ) × е рt = -10× е -20 t А. Знак «минус» у тока означает его обратное направление на схеме.
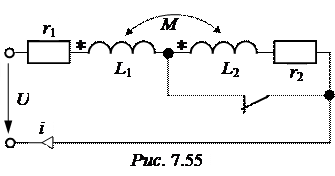
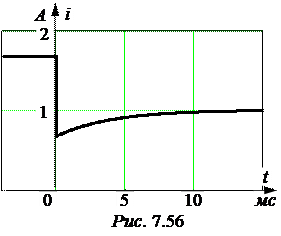
ЗАДАЧА 7.36. Рассчитать ток первой катушки в схеме рис. 7.55 со следующими числовыми данными: U = 100 В, r 1 = 60 Ом, r 2 = 40 Ом, L 1= 0,1 Гн, L 2= 0,2 Гн, М = 0,05 Гн. Построить график то-ка в первой катушке.
Решение
1. До коммутации в катушках были разные токи: в первой катушке – i 1 ( 0- ) = 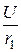 =
= 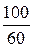 = 1,667 А, во второй катушке тока не было – i 2 ( 0- ) = 0.
= 1,667 А, во второй катушке тока не было – i 2 ( 0- ) = 0.
Таким образом, потокосцепление цепи до коммутации, состоящее из суммы потокосцеплений катушек
Y( 0- ) = Y 1 ( 0- ) + Y 2 ( 0- ) = L 1 i 1 ( 0- ) + Мi 2 ( 0- ) + L 2 i 2 ( 0- ) + Мi 1 ( 0- ) =
= 0,1×1,667 + 0 + 0 + 0,05×1,667 = 0,25 Вб.
Независимое начальное условие в соответствии с первым законом коммутации: Y( 0+ ) = Y( 0- ) = 0,25 Вб. Но потокосцепление цепи после комму-тации с учётом того, что катушки соединены последовательно согласно и по ним протекает один ток, равно Y( 0+ ) = i( 0+ ) × (L 1 + L 2 + 2 М). Отсюда
i( 0 ) = 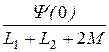 =
= 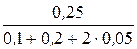 = 0,625 А.
= 0,625 А.
2. Принуждённая составляющая тока: iпр = 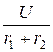 =
= 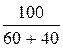 = 1 А.
= 1 А.
3. Характеристическое уравнение: р × (L 1 + L 2 + 2 М) + r 1 + r 2 = 0,
р = - 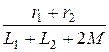 = -
= - 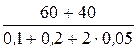 = -250 с -1.
= -250 с -1.
 4. Свободная составляющая тока
4. Свободная составляющая тока
iсв = А × е рt,
где постоянная интегрирования
А = iсв( 0 ) = i( 0 ) – iпр = 0,625 – 1 = -0,375.
5. Окончательно получаем:
i(t) = iпр(t) + iсв(t) = 1 – 0,375× е – 250 t А.
6. График тока приведен на рис. 7.56.
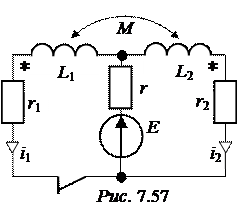 ЗАДАЧА 7.37. Рассчитать ток второй катушки в схеме рис. 7.57 со сле-дующими числовыми данными: Е = 11,7 В, r 1 = 1 Ом, r 2 = 9 Ом, r = 3 Ом, L 1= 10 мГн, L 2= 20 мГн, М = 10 мГн.
ЗАДАЧА 7.37. Рассчитать ток второй катушки в схеме рис. 7.57 со сле-дующими числовыми данными: Е = 11,7 В, r 1 = 1 Ом, r 2 = 9 Ом, r = 3 Ом, L 1= 10 мГн, L 2= 20 мГн, М = 10 мГн.
Решение
1. До коммутации
r = r + 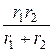 = 3 +
= 3 + 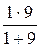 = 3,9 Ом,
= 3,9 Ом,
i 1 ( 0- ) = 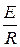 ×
× 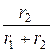 =
= 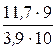 = 2,7 А,
= 2,7 А,
i 2 ( 0- ) = 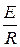 ×
× 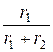 =
= 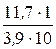 = 0,3 А.
= 0,3 А.
2. Уравнение для контура со второй катушкой по второму закону Кирхгофа для момента коммутации:
r × (i 1 + i 2 ) + r 2× i 2 + L 2 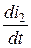 + М
+ М 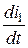 = Е или L 2 di 2=- Mdi 1
= Е или L 2 di 2=- Mdi 1
или L 2× (i 2 ( 0+ ) – i 2 ( 0- )) =- M × (i 1 ( 0+ ) – i 1 ( 0- )).
Но i 1 ( 0+ ) = 0, тогда i 2 ( 0+ ) = 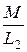 i 1 ( 0- ) + i 2 ( 0- ) =
i 1 ( 0- ) + i 2 ( 0- ) = 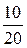 ×2,7 + 0,3 = 1,65 А.
×2,7 + 0,3 = 1,65 А.
3. Принуждённая составляющая тока i 2 пр = 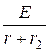 =
= 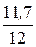 = 0,975 А.
= 0,975 А.
4. Корень характеристического уравнения
р = - 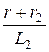 = -
= - 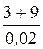 = -600 с -1.
= -600 с -1.
5. Свободная составляющая тока i 2 св = А × е рt,
где постоянная интегрирования А = i 2 св ( 0 ) = i 2 ( 0 ) – i 2 пр = 1,65 – 0,975 = 0,675.
6. Окончательно получаем: i 2 (t) = i 2 пр (t) + i 2 св (t) = 0,975 + 0,675× е – 600 t А.
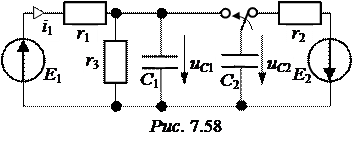
ЗАДАЧА 7.38. Рассчитать переходный ток i 1 (t) в схеме рис. 7.58 со следующими числовыми данными: Е 1= 36 В, Е 2= 6 В,
r 1 = 300 Ом, r 2 = r 3 = 600 Ом, С 1= 300 мкФ, С 2= 200 мкФ.
Решение
До коммутации напряжения и суммарный заряд конденсаторов:
uС 1 ( 0- ) = 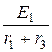 × r 3 =
× r 3 = 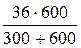 = 24 B, uС 2 ( 0- ) = - Е 2= -6 В.
= 24 B, uС 2 ( 0- ) = - Е 2= -6 В.
q( 0- ) = С 1 uС 1 ( 0- ) + С 2 uС 2 ( 0- ) = ( 300×24 – 200×6 ) ×10 -6 = 60×10 -4 Кл.
После коммутации конденсаторы будут находиться под одним напряжением uС( 0+ ) = uС 1 ( 0+ ) = uС 2 ( 0+ ). Поэтому заряд конденсаторов после коммутации q( 0+ ) = (С 1 + С 2 ) × uС( 0+ ). Но в соответствии со вторым законом коммутации q( 0+ ) = q( 0- ). Отсюда
uС( 0+ ) = 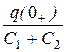 =
= 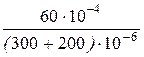 = 12 B.
= 12 B.
Начальное значение искомого тока
i 1 ( 0 ) = 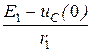 =
= 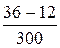 = 0,08 А = 80 мА.
= 0,08 А = 80 мА.
Принуждённый ток i 1 пр = 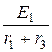 =
= 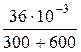 = 40 мА.
= 40 мА.
Свободный ток i 1 св = А × е рt, где корень характеристического уравнения
р = - 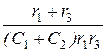 = -
= - 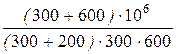 = -10 с –1,
= -10 с –1,
постоянная интегрирования А = i 1 св ( 0 ) = i 1 ( 0 ) – i 1 пр = 80 – 40 = 40.
Окончательно записываем: i 1 (t) = i 1 пр (t) + i 1 св (t) = 40 + 40× е – 10 t мА.
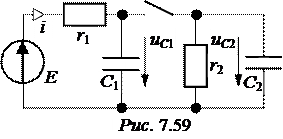 ЗАДАЧА 7.39. В схеме рис. 7.59 найти закон изменения тока источника ЭДС при замыкании контакта. Числовые данные: Е = 60 В, r 1 = r 2 = 1 кОм,
ЗАДАЧА 7.39. В схеме рис. 7.59 найти закон изменения тока источника ЭДС при замыкании контакта. Числовые данные: Е = 60 В, r 1 = r 2 = 1 кОм,
С 1= 1 мкФ, С 2= 2 мкФ.
Ответы: uС 1 ( 0+ ) = uС 2 ( 0+ ) = 20 В,
i(t) = 30 + 10× е – 667 t мА.
7.1.5. Метод переменных состояния (МПС)
Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле – это система дифференциальных уравнений первого порядка, разрешённая относительно производных. МПС – анализ цепи, основанный на решении уравнений состояния, записанных в форме Коши.
В электрических цепях токи в индуктивностях и напряжения на ёмкостях определяют энергетическое состояние цепи, поэтому их целесообразно взять в качестве переменных состояния – xk(t): [ X ] – матрица-столбец (размера k) переменных состояния.
Действующие источники называются входными величинами – Fl(t):
[ F ] – матрица-столбец (размера l) ЭДС и токов источников (внешних возмущений); искомые величины (остальные токи и напряжения) – выходные величины Wm(t): [ W ] – матрица-столбец размера m.
Сокращённо дифуравнения состояния записываются в матричной форме: 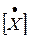 = [ K ] ´ [ X ] + [ L ] ´ [ F ],
= [ K ] ´ [ X ] + [ L ] ´ [ F ],
где [ K ] – квадратная матрица порядка k (основная), [ L ] – матрица связи разме-ра k ´ l. Элементы этих матриц определяются топологией и параметрами цепи.
Для выходных величин: [ W ] = [ M ] ´ [ X ] + [ N ] ´ [ F ],
где [ M ] – матрица связи размера m ´ k, [ N ] – матрица связи размера m ´ l.
Согласно классическому методу токи и напряжения находятся в виде суммы принуждённых и свободных составляющих:
iL(t) = iLпр(t) + iLсв(t); uC(t) = uCпр(t) + uCсв(t).
Методика определения принуждённых составляющих следующая:
- если источники постоянные, то производные от принуждённых составляющих равны нулю: 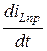 = 0,
= 0, 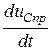 = 0. Уравнения состояния принимают вид: 0 = [ K ] ´ [ Xnp ] + [ L ] ´ [ F ],
= 0. Уравнения состояния принимают вид: 0 = [ K ] ´ [ Xnp ] + [ L ] ´ [ F ],
- если источники синусоидальные – удобно перейти к комплексам:
jw [ X np ] = [ K ] ´ [ X np ] + [ L ] ´ [ F ].
Система уравнений даёт возможность удобно составить характеристическое уравнение. Для этого систему нужно алгебраизировать и её определитель, состоящий из коэффициентов при переменных состояния, приравнять к нулю. Составлять характеристическое уравнение через входное сопротивление в операторной форме целесообразно лишь в цепочных схемах, где нет мостиковых соединений ветвей и индуктивных связей. Непосредственно из системы уравнений можно получить начальные значения производных от переменных состояния, подставив в систему независимые начальные условия. Эти начальные значения используются при нахождении постоянных интегрирования.
Система уравнений состояния может также решаться матричным способом с помощью программируемой вычислительной техники. Примеры – см. задачи 7.43 и 7.44.
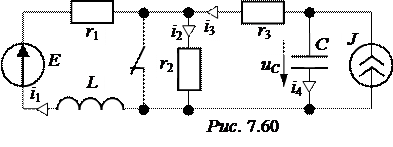
ЗАДАЧА 7.40. Рассчитать токи переходного процесса в схеме рис. 7.60 методом переменных состояния. Числовые значения: Е = 100 В, J = 5 A, r 1 = 20 Ом, r 2 = 30 Ом, r 3 = 10 Ом, L = 0,09 Гн, C = 100 мкФ.
 Решение
Решение
1. Назначаем в каче-стве переменных состояния ток в индуктивности и напряжение на конденсато-ре – i 1 (t) и uC(t). Выходные переменные – остальные токи: i 2 (t), i 3 (t), i 4 (t).
 2. Независимые начальные условия:
2. Независимые начальные условия:
i 1 ( 0+ ) = i 1 ( 0- ) = 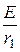 =
= 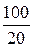 = 5 А,
= 5 А,
uC( 0+ ) = uC( 0- ) = J × r 3 = 5×10 = 50 В.
3. Для переменных состоя-ния составим систему дифферен-циальных уравнений в форме Коши. Производные i 1¢ (t) и uC ¢ (t) получим, соответственно, из uL = Li 1¢ (t) и i 4= CuC ¢ (t). Для нахождения uL и i 4в исходной схеме заменим индуктивность источником тока i 1, а емкость – источником напряжения uC. В резистивной цепи рис. 7.61 определим uL и i 4, а также выходные переменные i 3 (t) и i 2 (t). Это можно сделать любым методом расчёта сложных цепей постоянного тока. выполним расчёт методом контурных токов. Имеем три независимых контура с двумя известными токами i 1 и J и с одним неизвестным i 3. Составляем одно уравнение: (r 2+ r 3 ) × i 3+ r 2× i 1 = uC.
Решение уравнения: i 3= 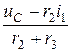 =
= 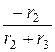 × i 1 +
× i 1 + 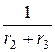 × uC.
× uC.
Остальные расчётные величины:
i 2 = i 1 + i 3 = 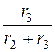 × i 1 +
× i 1 + 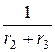 × uC;
× uC;
i 4 = С 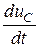 = J – i 3 =
= J – i 3 = 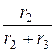 × i 1 –
× i 1 – 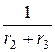 × uC + J;
× uC + J;
uL = L 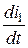 = Е – r 1× i 1 – r 2× i 2 = - (r 1+
= Е – r 1× i 1 – r 2× i 2 = - (r 1+ 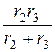 ) × i 1 –
) × i 1 – 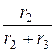 × uC + Е.
× uC + Е.
Из последних двух уравнений получаем уравнения состояния в форме Коши:
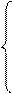
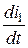 = -
= - 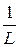 (r 1+
(r 1+ 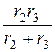 ) × i 1 –
) × i 1 – 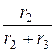 ×
× 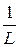 uC +
uC + 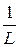 Е;
Е;
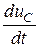 =
= 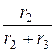 ×
× 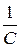 i 1 –
i 1 – 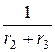 ×
× 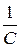 uC +
uC + 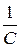 J.
J.
Остальные полученные уравнения называются уравнениями связи. Они нужны для нахождения выходных переменных.
4. Систему уравнений состояния решим классическим методом:
i 1 (t)= i 1 пр (t) + i 1 св (t); uC (t)= uCпр(t) + uCсв(t).
Поскольку в цепи действуют постоянные источники, принуждённые составляющие являются также постоянными, а производные от них равны нулю. В соответствии с принципом наложения система уравнений состояния оказывается справедливой не только для полных i 1 (t) и uC (t), но и для их составляющих. Система уравнений состояния для принуждённых составляющих, таким образом, имеет вид:
 - (r 1+
- (r 1+ 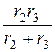 ) × i 1 пр –
) × i 1 пр – 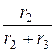 × uCпр = - Е; или -27,5× i 1 пр – 0,75× uCпр = -100;
× uCпр = - Е; или -27,5× i 1 пр – 0,75× uCпр = -100;
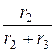 × i 1 пр –
× i 1 пр – 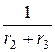 × uCпр = - J. 0,75× i 1 пр – 0,025× uCпр = -5.
× uCпр = - J. 0,75× i 1 пр – 0,025× uCпр = -5.
Решение системы: i 1 пр = -1 А, uCпр = 170 В.
5. Алгебраизировав уравнения состояния и приравняв определитель системы уравнений к нулю, получим характеристическое уравнение:
D(р) = 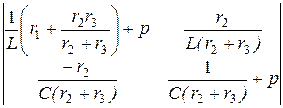 =
=
= р 2 + 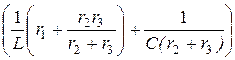 × р +
× р + 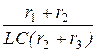 = р 2 + 555,6 р + 138900 = 0.
= р 2 + 555,6 р + 138900 = 0.
Корни характеристического уравнения: р 1,2 = -277,8 ± j 248,5 с -1.
Свободные составляющие имеют вид:
i 1 св (t) = А × е -a×t × sin(wt + Y 1 ); uCсв(t) = B × е -a×t × sin(wt + Yu),
Здесь a = | Re(р 1 ) | = -277,8 с –1 – коэффициент затухания,
w = Im(р 1 ) = 248,5 с –1 – угловая частота свободных колебаний.
Начальные значения свободных составляющих и их производных:
i 1 св ( 0 ) = А × sinY 1; i 1 св ¢ ( 0 ) = -a × А × sinY 1 + w × А × cosY 1;
uCсв( 0 ) = B × sinYu; uCсв ¢ ( 0 ) = -a × B × sinYu + w × B × cosYu.
6. Независимые начальные условия: i 1 ( 0 ) = 5 А, uC( 0 ) = 50 В.
Начальные значения производных получим из уравнений состояния:
i 1¢ ( 0 ) = - 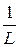 (r 1+
(r 1+ 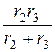 ) × i 1 ( 0 ) –
) × i 1 ( 0 ) – 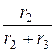 ×
× 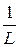 uC( 0 ) +
uC( 0 ) + 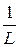 Е =
Е =
= - 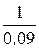 ×27,5×5 – 0,75×
×27,5×5 – 0,75× 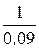 ×50 +
×50 + 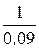 ×100 = -833,3 А / с.
×100 = -833,3 А / с.
uC ¢ ( 0 ) = 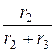 ×
× 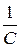 i 1 ( 0 ) –
i 1 ( 0 ) – 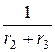 ×
× 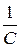 uC ( 0 ) +
uC ( 0 ) + 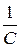 J =
J =
= 0,75×10 4×5 – 0,025×10 4×50 + 10 4×5 = 75000 В / с.
Начальные значения свободных составляющих и их производных:
i 1 св( 0 ) = i 1 ( 0 ) – i 1 пр = 5 + 1 = 6 А, i 1 св ¢ ( 0 ) = i 1¢ ( 0 ) – i 1 пр ¢ = -833,3 А / с,
uCсв( 0 ) = uC( 0 ) – uCпр = 50 – 170 = -120 В, uCсв ¢ ( 0 ) = uC ¢ ( 0 ) – uCпр ¢= 75000 В / с.
Получаем и решаем следующие системы уравнений:
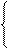
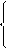 А × sinY 1 = 6, B × sinYu = -120,
А × sinY 1 = 6, B × sinYu = -120,
- a × А × sinY 1 + w × А × cosY 1 = -833,3; - a × B × sinYu + w × B × cosYu = 75000.
А = 6,874, Y 1 = 60,8°, B = 452,1, Yu = -15,4°.
7. Окончательные выражения для переменных состояния:
i 1 (t)= i 1 пр (t) + i 1 св (t) = -1 + 6,874× е –277,8 t × sin( 248,5 t + 60,8° ) А;
uC (t)= uCпр(t) + uCсв(t) = 170+ 452,1× е –277,8 t × sin( 248,5 t – 15,4° ) В.
8. Выходные переменные:
i 2 (t) = 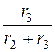 × i 1 +
× i 1 + 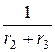 × uC = 0,25× i 1 + 0,025× uC =
× uC = 0,25× i 1 + 0,025× uC =
= 4 + 11,83× е –277,8 t × sin( 248,5 t – 7,29° ) А;
i 3 (t) = 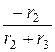 × i 1 +
× i 1 + 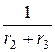 × uC = -0,75× i 1 + 0,025× uC =
× uC = -0,75× i 1 + 0,025× uC =
= 5 + 11,25× е –277,8 t × sin( 248,5 t – 41,83° ) А;
i 4 (t) = 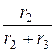 × i 1 –
× i 1 – 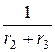 × uC + J = 0,75× i 1 – 0,025× uC + 5 =
× uC + J = 0,75× i 1 – 0,025× uC + 5 =
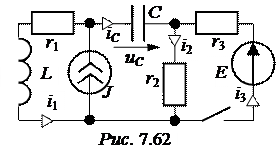 = 11,25× е – 277,8 t × sin( 248,5 t + 138,17° ) А.
= 11,25× е – 277,8 t × sin( 248,5 t + 138,17° ) А.
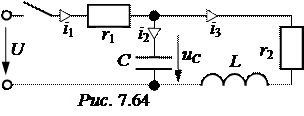
ЗАДАЧА 7.41. Рассчитать токи пере-ходного процесса, напряжения на индук-тивности и ёмкости в цепи рис. 7.62, если Е = 240 В, J = 4 A, r 1 = 80 Ом, r 2 = 120 Ом, r 3 = 120 Ом, L = 0,5 Гн, C = 10 мкФ.
Ответы: uC(t)= 200 + 126,3× е – 140 t × sin( 424,7 t + 71,75° ) B;
i 1 (t) = 4 – 0,565× е – 140 t × sin( 424,7 t) А; i 2 (t) = 1 – 0,283× е – 140 t × sin( 424,7 t) А;
i 3 (t) = 1 + 0,283× е – 140 t × sin( 424,7 t) А; iC(t) = -0,565× е – 140 t × sin( 424,7 t) А;
uL(t)= 120,1× е– 140 t × sin( 424,7 t + 92,7° ) B.
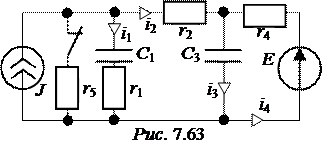
ЗАДАЧА 7.42. Определить токи переходного процесса в цепи рис. 7.63, если r 1 = r 4 = 200 Ом,
r 2 = r 5 = 100 Ом, C 1 = C 3 = 100 мкФ, Е = 300 В, J = 1 A.
Ответы:
 i 1 (t) = 0,8× е – 16,67 t – 0,3× е – 100 t А;
i 1 (t) = 0,8× е – 16,67 t – 0,3× е – 100 t А;
i 2 (t) = 1 – 0,8× е – 16,67 t + 0,3× е – 100 t А;
i 3 (t) = 0,4× е – 16,67 t + 0,6× е – 100 t А;
i 4 (t) = -1 + 1,2× е – 16,67 t + 0,3× е – 100 t А.
ЗАДАЧА 7.43. Построить графики токов i 1 (t) и i 3 (t) схемы рис. 7.64, при условии r 1 = 60 Ом, r 2 = 40 Ом, C = 100 мкФ, L = 0,1 Гн, u = 100 В.
Дата публикования: 2014-11-19; Прочитано: 663 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
