 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
функций произвольного периода
|
|
Разлагать в ряд Фурье можно и периодические функции с периодом отличным от 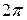 .
.
Пусть функция  , определенная на отрезке
, определенная на отрезке 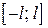 , имеет период
, имеет период 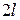 (
(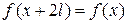 , где
, где 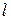 - произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
- произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
Сделав подстановку 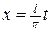 , данную функцию
, данную функцию  преобразуем в функцию
преобразуем в функцию 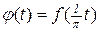 , которая определена на отрезке
, которая определена на отрезке 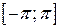 и имеет период
и имеет период 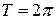 . Действительно, если
. Действительно, если 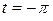 , то
, то 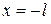 ; если
; если 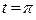 , то
, то 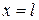 и при
и при 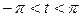 имеем
имеем 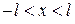 .
.
Разложение функции 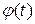 в ряд Фурье на отрезке
в ряд Фурье на отрезке 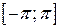 имеет вид:
имеет вид:
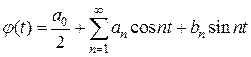 ,
,
где
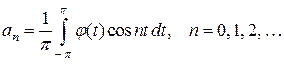
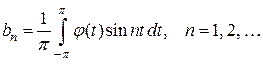 .
.
Возвращаясь к переменной 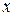 и заметив, что
и заметив, что 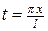 ,
, 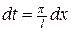 , получим
, получим
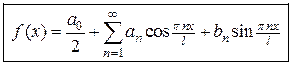 , (4.10)
, (4.10)
где
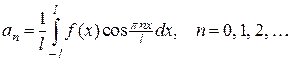 (4.11)
(4.11)
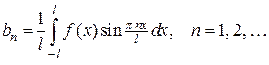 .
.
Ряд (4.10) с коэффициентами, вычисляемыми по формулам (4.11), называется рядом Фурье для функции  с периодом
с периодом  .
.
Все теоремы, имеющие место для рядов Фурье 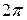 -периодических функций, остаются в силе и для рядов Фурье функций, период которых
-периодических функций, остаются в силе и для рядов Фурье функций, период которых  .
.
В частности, если функция  на отрезке
на отрезке 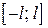 четная, то ее ряд Фурье имеет вид:
четная, то ее ряд Фурье имеет вид:
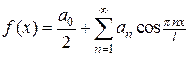 , (4.12)
, (4.12)
где  ,
,  ,
, 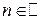 ;
;
если функция  - нечетная, то ряд Фурье имеет вид:
- нечетная, то ряд Фурье имеет вид:
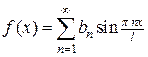 , (4.13)
, (4.13)
где 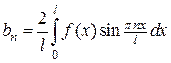 ,
, 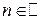 .
.
Дата публикования: 2014-11-19; Прочитано: 497 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
