Четных и нечетных функций

Если разлагаемая на отрезке 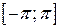в ряд Фурье функция является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).

Допустим, что разлагаемая в ряд Фурье функция - четная. Тогда функции будут нечетными и все коэффициенты 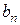, как интегралы от нечетных функций по интервалу 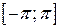, симметричному относительно начала координат, окажутся равными нулю. Функции будут четными.

Итак, если функция - четная, то ряд Фурье имеет вид (состоит из одних косинусов):

, (4.8)

где , , .

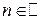Допустим, что разлагаемая в ряд Фурье функция - нечетная. Тогда функции будут нечетными и все коэффициенты 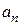, как интегралы от нечетных функций по интервалу 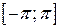, симметричному относительно начала координат, окажутся равными нулю. Функции будут четными.

Итак, если функция - нечетная, то ряд Фурье имеет вид (состоит из одних синусов):

, (4.9)

где , .

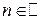Ряды (4.8) и (4.9) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.

Пример 4.2. Разложить в ряд Фурье функцию , .

Решение. Построим график функции :

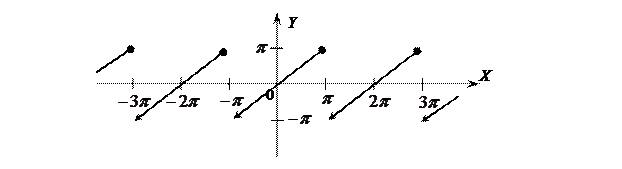
Эта функция удовлетворяет условиям теоремы Дирихле. Значит, ее можно разложить в ряд Дирихле.

Функция − нечетная. Следовательно, .

Находим коэффициент .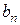

.

Таким образом,

,

или

.

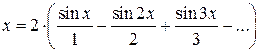В точках сумма ряда равна:

.

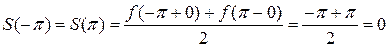График 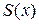имеет вид:

,