 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тригонометрический ряд Фурье
|
|
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.
Определение 4.1. Тригонометрическим рядом называется функциональный ряд вида
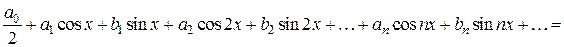
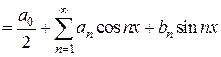 , (4.3)
, (4.3)
где действительные числа 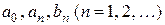 называются коэффициентами ряда.
называются коэффициентами ряда.
Свободный член ряда записан в виде 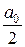 для единообразия получающихся в дальнейшем формул.
для единообразия получающихся в дальнейшем формул.
Приведем формулы, которые помогут найти коэффициенты ряда (4.3) 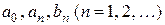 .
.
Считая  и
и 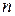 целыми положительными числами, находим:
целыми положительными числами, находим:
(1) Если 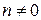 , то
, то  ;
;
Если 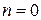 , то
, то 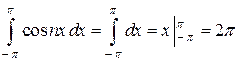 .
.
(2) При любом 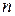
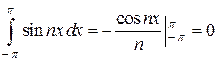 .
.
(3) Если 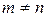 , то
, то
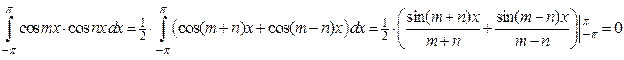 Если
Если 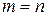 , то
, то
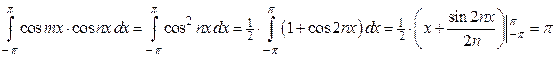 .
.
(4) При любых  и
и 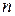
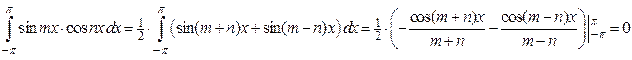
(5) Если 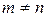 , то
, то
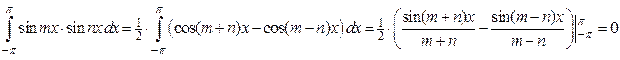
Если 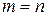 , то
, то
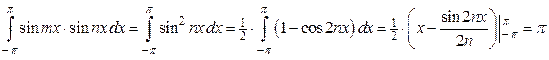 .
.
Замечания.
- Формулы (1) – (5) показывают, что семейство функций
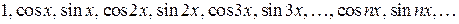
обладают свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 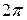 , равен нулю.
, равен нулю.
- Формулы (1) – (5) справедливы и в случае, когда область интегрирования есть отрезок
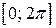 .
.
Пусть  - произвольная периодическая функция с периодом
- произвольная периодическая функция с периодом 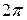 . Предположим, что функция
. Предположим, что функция  разлагается в тригонометрический ряд, т.е.
разлагается в тригонометрический ряд, т.е.  является суммой ряда:
является суммой ряда:
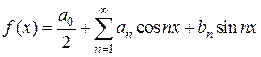 . (4.4)
. (4.4)
Так как функция  (и сумма ряда) имеет период
(и сумма ряда) имеет период 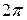 , то ее можно рассматривать в любом промежутке длины
, то ее можно рассматривать в любом промежутке длины 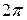 . В качестве основного промежутка возьмем отрезок
. В качестве основного промежутка возьмем отрезок 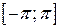 (также удобно взять отрезок
(также удобно взять отрезок 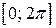 ) и предположим, что ряд (4.4) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты
) и предположим, что ряд (4.4) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты 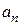 и
и 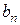 . Для этого проинтегрируем обе части равенства (4.4) в пределах от
. Для этого проинтегрируем обе части равенства (4.4) в пределах от 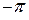 до
до 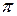 .
.
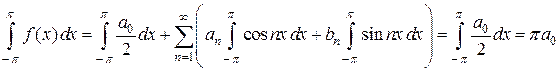 .
.
Интегралы от всех, кроме нулевых членов ряда равны нулю в силу формул (1) и (2).
Отсюда
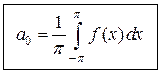 . (4.5)
. (4.5)
Умножив обе части равенства (4.4) на 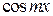 и проинтегрировав полученный ряд в пределах от
и проинтегрировав полученный ряд в пределах от 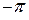 до
до 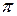 , получаем:
, получаем:
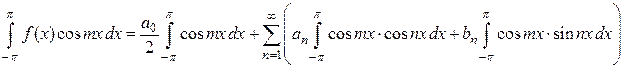
В силу формул (1), (3) и (4) из последнего равенства при 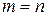 получаем:
получаем:
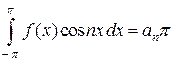 .
.
Отсюда
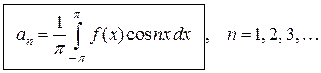 . (4.6)
. (4.6)
Аналогично, умножив равенство (4.4) на 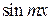 и проинтегрировав почленно на отрезке
и проинтегрировав почленно на отрезке 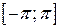 , найдем:
, найдем:
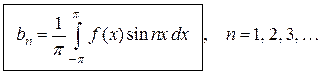 . (4.7)
. (4.7)
Итак, заранее предполагая, что функция  может быть разложена в тригонометрический ряд (4.4), мы сумели найти все его коэффициенты.
может быть разложена в тригонометрический ряд (4.4), мы сумели найти все его коэффициенты.
Определение 4.2. Ряд вида:
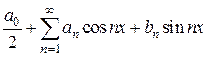
называется рядом Фурье функции  .
.
Коэффициентами Фурье функции  называются числа
называются числа 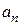 и
и 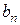 определяемые формулами
определяемые формулами
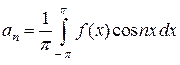 ,
, 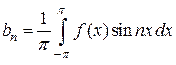 , где
, где 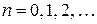 .
.
Дата публикования: 2014-11-19; Прочитано: 729 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
