Вычисление интегралов

Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри интервалов сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.

Пример 3.11. Вычислить с точностью .

Решение. Воспользуемся формулой разложения функции 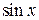в степенной ряд, заменив 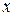на . Получаем ряд

.

Полученный ряд сходится на всей числовой прямой, поэтому его можно всюду почленно интегрировать. Следовательно,

,

Поскольку уже третий член полученного знакочередующегося ряда меньше .

,