 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример. a. ,так как , а степени многочленов в числителе и знаменателе одинаковые, следовательно предел равен отношению коэффициентов при старших степенях
|
|
Найти предел функции:
a. 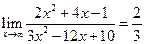 ,так как
,так как 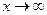 , а степени многочленов в числителе и знаменателе одинаковые, следовательно предел равен отношению коэффициентов при старших степенях.
, а степени многочленов в числителе и знаменателе одинаковые, следовательно предел равен отношению коэффициентов при старших степенях.
b. 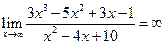 ,так как
,так как 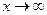 , а степень многочлена в числителе больше, чем степень многочлена в знаменателе.
, а степень многочлена в числителе больше, чем степень многочлена в знаменателе.
c. 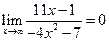 ,так как
,так как 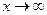 , а степень многочлена в знаменателе больше, чем степень многочлена в числителе.
, а степень многочлена в знаменателе больше, чем степень многочлена в числителе.
Пример. Найти предел функции.
a. 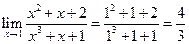
b. 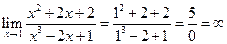
c. 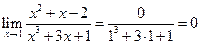
d. 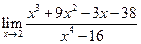 Следующий пример дает неопределенность
Следующий пример дает неопределенность 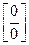 поэтому число 2 является корнем многочлена, стоящего в числителе и знаменателе. Тогда эти многочлены можно разложить на множители. По формуле разности квадратов
поэтому число 2 является корнем многочлена, стоящего в числителе и знаменателе. Тогда эти многочлены можно разложить на множители. По формуле разности квадратов
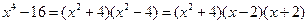
Для разложение многочлена, стоящего в числителе на множители мы можем применить метод группировки или поделить многочлен на многочлен «в столбик».
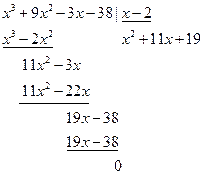
Тогда получим 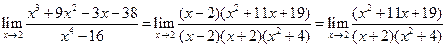
Полученная дробь уже не дает неопределенности и для вычисления ее предела мы можем подставить число 2:
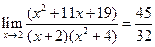
Пример. Вычислить пределы:
a. 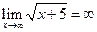
b. 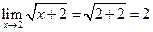 предел непрерывной функции равен значению функции в этой точке.
предел непрерывной функции равен значению функции в этой точке.
c. 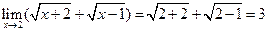 предел непрерывной функции равен значению функции в этой точке.
предел непрерывной функции равен значению функции в этой точке.
d. 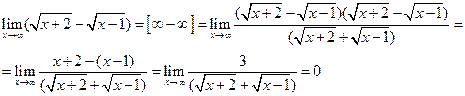
В случае неопределенности типа 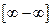 нужно перейти к неопределенности типа
нужно перейти к неопределенности типа 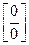 или
или 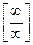 , для этого домножим числитель и знаменатель дроби на сопряженное выражение.
, для этого домножим числитель и знаменатель дроби на сопряженное выражение.
e. 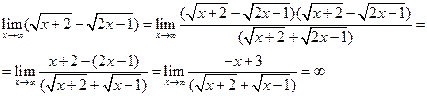 так как степень числителя больше степени знаменателя, то по рассмотренному ранее правилу мы получаем, что предел равен бесконечности..
так как степень числителя больше степени знаменателя, то по рассмотренному ранее правилу мы получаем, что предел равен бесконечности..
Пример. Вычислить пределы:
a) 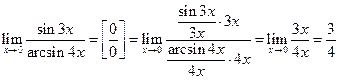 При подстановке значения переменно получается неопределенность типа
При подстановке значения переменно получается неопределенность типа 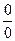 , поэтому непосредственной подстановкой результат вычислений быть получен не может. Поэтому для его вычисления используем первый замечательный предел и следствие из него.
, поэтому непосредственной подстановкой результат вычислений быть получен не может. Поэтому для его вычисления используем первый замечательный предел и следствие из него.  , где
, где 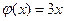 ,
, 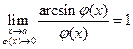 , где
, где 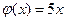 .
.
b) 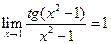 . При непосредственной подстановки значения переменной получается неопределенность типа
. При непосредственной подстановки значения переменной получается неопределенность типа 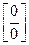 . Данный предел является непосредственным первого замечательного предела, где в качестве
. Данный предел является непосредственным первого замечательного предела, где в качестве 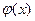 берется функция
берется функция  .
.
c) 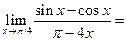 при подстановке значения переменной получается неопределенность типа
при подстановке значения переменной получается неопределенность типа 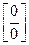 , поэтому для вычисления предела необходимы дополнительные преобразования:
, поэтому для вычисления предела необходимы дополнительные преобразования: 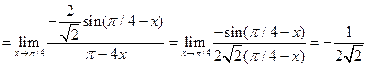
d) 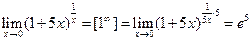 При непосредственном вычислении получается неопределенность типа
При непосредственном вычислении получается неопределенность типа 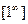 , поэтому для его вычисления мы воспользовались вторым замечательным пределом
, поэтому для его вычисления мы воспользовались вторым замечательным пределом
e) 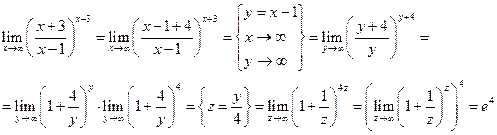
Дата публикования: 2014-11-18; Прочитано: 521 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
