Решение. 1. Вычислим расстояние между точками

1. Вычислим расстояние между точками

.

2. Угол между векторами вычислим используя формулу для скалярного произведения.

Подставляя в формулу получим .

3. Угол между ребром и плоскостью вычисляется по формуле:

, где - вектор нормали к плоскости, - направляющий вектор прямой.

Направляющий вектор прямой совпадает с вектором и, следовательно с учетом предыдущего пункта .

Для нахождения вектора, ортогонального плоскости, нам надо найти вектор ортогональный двум векторам из (ABC), в качестве таких векторов возьмем и .

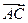Вектор, полученный в результате векторного произведения этих векторов и будет искомым вектором.

, .

.

Поставляя в формулу получим: .

4. Для нахождения тетраэдра воспользуемся формулой через смешанное произведение.

, ,

Вычисляя смешанное произведение получим

.

5. Для нахождения уравнения мы можем воспользоваться формулой для вычисления прямой через две точки.

6. Для нахождения уравнения плоскости воспользуемся формулой, для нахождения плоскости, проходящей через три точки.

Получаем:

.

7. Для нахождения высоты, нам необходимо знать направляющий вектор, в качестве которого можно взять вектор нормали и точку, через которую проходит высота.

, D(-5,-4,8).

Тогда уравнение высоты имеет вид:

.

8. Для нахождения точки пересечения высоты с плоскостью запишем уравнение высоты в параметрическом виде:

Подставляя в уравнение плоскости получим

Откуда

И, подставляя в параметрическое задание прямой, получаем координаты точки пересечения:

9. Длину высоты можно вычислить как расстояние между точками D и O. Получим:

.

Тема: «Предел функции»

Вопросы:

- Понятие предела.

- Свойства пределов.

- Первый и второй замечательный предел.

- Правила вычисления пределов.

В результате изучения темы слушатели должны уметь:

- Вычислять пределы.

Эти вопросы рассмотрены в [1],[3],[5] и в [2],[3],[5] приведены примеры решений типовых задач.

[1] Глава 4. Функции одной переменной. Стр. 69-103.

Глава 11. Предел и непрерывность функций нескольких переменных. Стр. 275-283.

[2] Глава 11. Понятие, предел и непрерывность функций нескольких переменных. Стр. 179-183.

[3] Глава 5. Введение в анализ. Стр. 97-185.

[5] Глава 6. Введение в анализ. Стр. 172-189.