Примеры. Воспользуемся подстановкой x=t2

1. Найти интеграл

Решение:

Воспользуемся подстановкой x=t². Тогда , получим

2.

Воспользуемся подстановкой cosx=t. Тогд а -sindx=dt

З а м е ч а н и е. Можно интегрирование методом подстановки оформить так:

3.

4.

=

5.

6

П р о в е р к а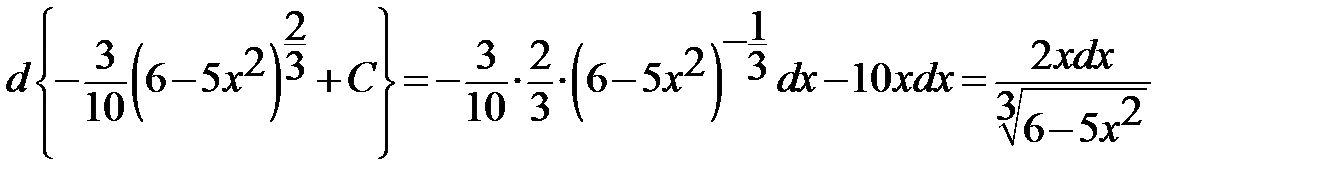

7.

Интегрирование по частям

Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции. Тогда справедлива формула

.

Чтобы применить его в каком – нибудь данном случае, нужно уметь разбить заданное дифференциальное выражение на два множителя, именно: на u и на dv. Общих правил для этого, к сожалению, никак нельзя дать, кроме, как можно интегралы условно можно разбить на группы:

1. , ,

логарифм, логарифм, умноженный на какой – либо многочлен.

2. ,

экспонциальная функция, умноженная на какой – либо многочлен.

3. ,

тригонометрические функции, умноженные на какой – либо многочлен.

4. ,

обратные тригонометрические функции,»арки», умноженные на многочлен.

5.Также по частям берутся некоторые дроби.