 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
|
|
Общее правило: за u всегда обозначается обратная тригонометрическая функция!
11. 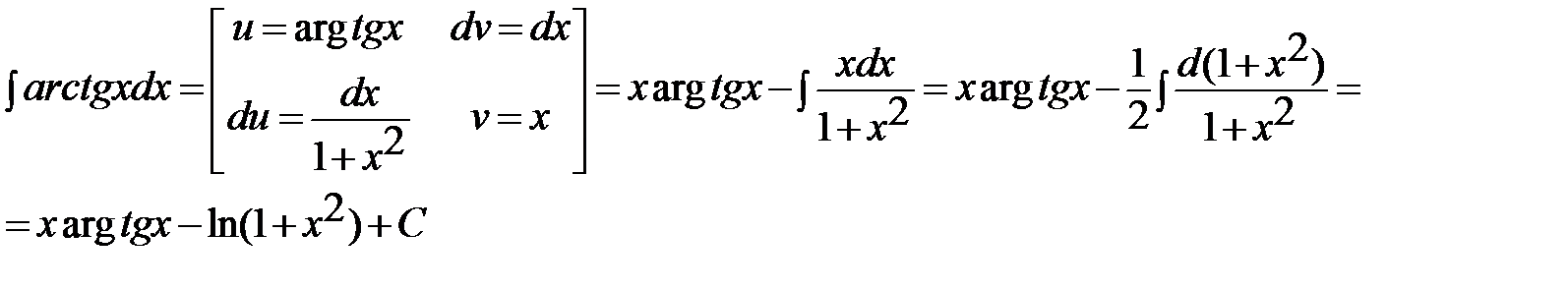
 Интегрирование простейших рациональных дробей
Интегрирование простейших рациональных дробей
Многочленом степени n называется выражение вида  , где
, где  – действительные числа
– действительные числа 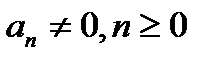 . Например, 5–7x – многочлен первой степени
. Например, 5–7x – многочлен первой степени 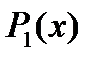 ,
,
 =2x3 – 3x2 +8x – 1 – многочлен третьей степени.
=2x3 – 3x2 +8x – 1 – многочлен третьей степени.
Рациональной дробью называется отношение двух многочленов. Например,  – рациональные дроби. Всякая рациональная дробь имеет вид:
– рациональные дроби. Всякая рациональная дробь имеет вид:

где  – многочлены степени m и n соответственно.
– многочлены степени m и n соответственно.
 , если
, если 


Простейшими рациональными дробями являются следующие четыре типа дробей:
I)  ; II)
; II)  III)
III)  ; IV)
; IV) 
Очевидно, что интегралы от простейших дробей первого и второго типов находятся легко:
 ,
,

где k – целое, 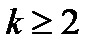 .
.
От дробей третьего и четвёртого типов вычисляют заменой  , или по следующим формулам:
, или по следующим формулам:


 Разложение многочленов на множители
Разложение многочленов на множители
Для любых многочленов  имеет место теорема Безу:
имеет место теорема Безу:
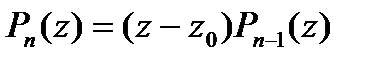 , где z0 - простой корень
, где z0 - простой корень
 , где z0 - корень кратности k.
, где z0 - корень кратности k.
Если z - корень комплексный:  , где i=
, где i= 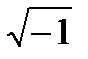
и  , то
, то  , где
, где  – сопряженный корень.
– сопряженный корень.
Любой многочлен можно разложить на линейные и квадратичные множители


 – действительные корни;
– действительные корни;  - комплексные корни
- комплексные корни
Правильную рациональную дробь можно разложить на сумму простейших дробей, если знаменатель дроби  представлен в виде сомножителей
представлен в виде сомножителей 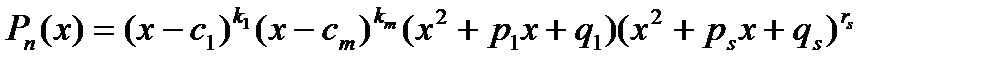 :
:

12. Разложить на сумму простейших дробей следующие дроби:
а)  ;
;
б)  .
.
Решение:
а) 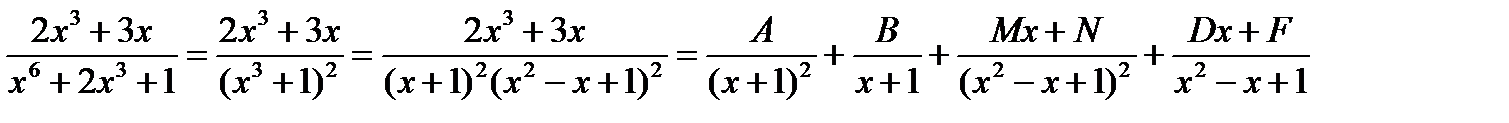
б) 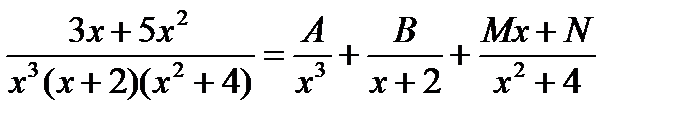
13. Вычислить интеграл:

Решение:
Разложим подынтегральную дробь на простейшие дроби

приравнивая числители дробей, получаем:

Определим коэффициенты А и В, придавая любые значения переменной x:

Получаем А=1 и В=1. Исходный интеграл найдём как сумму интегралов от полученных дробей.

 Интегрирование тригонометрических функций
Интегрирование тригонометрических функций
 Рассмотрим интегралы вида
Рассмотрим интегралы вида 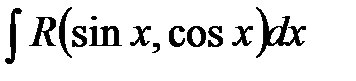 . Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной
. Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной  , где
, где 
Такая замена называется универсальной тригонометрическая подстановкой.
В этом случае,



Тогда
 .
.
14. Найти 
Решение:
Положим 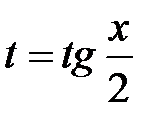 . Тогда, используя выражения через t для dx и sin x, указанные выше, получаем, что искомый интеграл равен
. Тогда, используя выражения через t для dx и sin x, указанные выше, получаем, что искомый интеграл равен

 При вычислении интегралов вида
При вычислении интегралов вида

рассмотрим частные случаи:
n – нечётное
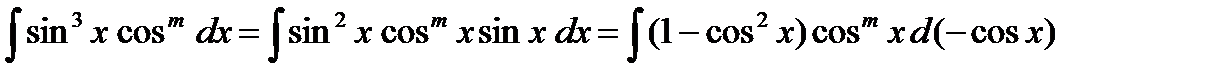
n, m – чётные,  .
.
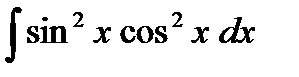
применяют формулы тригонометрии:


 При вычислении интегралов вида
При вычислении интегралов вида  делают замену
делают замену  , тогда
, тогда



 Если интеграл имеет вид
Если интеграл имеет вид
 ,
,
где n, m – чётные, применяют формулу:

15. Вычислить интегралы:
а) 
б) 
Решение:
а) 
б) 
 При вычислении
При вычислении
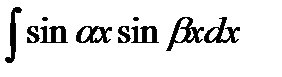


используют формулы



 Интегрирование иррациональных выражений
Интегрирование иррациональных выражений
При вычислении интегралов, содержащих иррациональные выражения применяют замену переменной.
Если  ,
,
то  , где
, где 

Если 
то 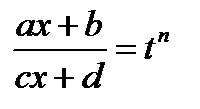 , где
, где 
Дата публикования: 2014-11-03; Прочитано: 1856 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
