Замена плоскостей проекций

Сущность способа заключается в следующем: 1) Положение геометрического объекта не меняется по отношению к старой системе плоскостей проекций; 2) Новая система взаимно перпендикулярных плоскостей проекций выбирается так, чтобы рассматриваемый геометрический объект оказался бы в частном положении по отношению к одной из плоскостей новой системы; 3) Направление проецирования сохраняется ортогональным.

На рис.4.1 показана схема построения новых (дополнительных) проекций точек
А и В.

В системе плоскостей проекций П₂ ^ П₁ заданы точки А(А₁, А₂) и В(В_1, В₂).

Для замены фронтальной плоскости проекций введена новая плоскость П₄ ^ П₁. Расстояние от точки А до плоскости П₁ при замене не меняется: Z_A = const, A₁ = const. Проекция А₄ точки а на плоскость П₄ находится на линии проекционной связи, перпендикулярной дополнительной оси Х₁₄, на расстоянии Z_А от нее, равном расстоянию от точки А до плоскости проекций П₁. Z_А определяется по основному чертежу как расстояние от проекции А₂ до оси X_12­.

Для замены горизонтальной плоскости проекций введена новая плоскость проекций П₅ ^ П₂. Расстояние от точки В до неизменной плоскости проекций П₂ не изменяется: Y_B = const, B₂ = const. Проекция В₅ на плоскость П₅ находится на линии проекционной связи, перпендикулярной новой оси координат Y_25, на расстоянии Y_А от нее.

Рис. 4.1

Замена одной из плоскостей проекций не всегда приводит к решению задачи. Иногда приходится заменять две и более плоскостей проекций.

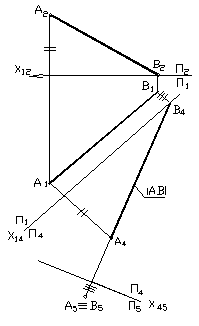
Пример 4.1. Перевести отрезок прямой АВ из общего положения в проецирующее. (рис. 4.2).

Первая система плоскостей проекций. Перейдем от системы плоскостей П₁ ^ П₂ к системе П₁ ^ П₄, заменив П₂ на П₄ так, чтобы АВ || П_4. Новая ось X₁₄ проведена параллельно проекции А₁В₁, при этом
П₄ || АВ. Из А₁ и В₁ перпендикулярно X₁₄ проведем линии проекционной связи, на них отложим отрезки, равные Z_A и Z_В. Получим новую проекцию, равную натуральной величине отрезка - А₄В₄=|АВ|.

Вторая замена плоскостей проекций. Плоскость П₁ заменяем на П₅ так, чтобы отрезок АВ стал проецирующим - АВ ^ П₅. Для этого проведем новую ось X₄₅ ^ А₄В₄ и на линии проекционной связи, являющейся продолжением проекции отрезка А₄В₄, отложим отрезки, равные расстояниям от заменяемой оси координат X₁₄. Так как эти отрезки равны, то получаем одну точку
А₅ º В_5, являющуюся проекцией отрезка АВ на плоскость П₅.

Рис. 4.2

Рис. 4.2

Пример 4.2. Найти натуральную величину ∆ АВС и угол наклона его плоскости к плоскости проекций П₁ (рис. 4.3).

Рис. 4.3

Выберем новую плоскость проекций П₄, перпендикулярную плоскости треугольника АВС, а на чертеже – перпендикулярную горизонтали АК плоскости треугольника - П₄ ^ ∆ АВС, П₄ ^ АК, АК Î ∆АВС, АК || П₁.Проводим новую ось координат X₁₄ ^ А₁К₁. Имеем систему взаимно перпендикулярных плоскостей П₁ ^ П₄. Плоскость ∆ АВС по отношению к плоскости П₄ будет проецирующей. Проводим линии проекционной связи от точек А₁, В₁ и С₁ и откладываем координаты Z вершин треугольника от новой оси X₁₄, получаем проекции точек А_4, В₄, С₄. Проекции ∆ АВС на П₄ – прямая С₄ В₄, составляющая с осью X₁₄ угол, равный натуральной величине угла между плоскостью треугольника и плоскостью П₁ – угол φ.

Чтобы найти натуральную величину треугольника вместо плоскости П₁ вводим новую плоскость П₅ плоскости треугольника. Параллельно проекции треугольника С₄ В₄ проводим новую ось X₄₅. На линиях проекционной связи отложим от новой оси отрезки, равные расстояниям от заменяемых проекций вершин А₁, В₁, С₁ до заменяемой оси X₁₄. А₅В₅С₅ – натуральная величина треугольника. А₅В₅С₅ = |АВС|

Задача 4.1. Определить натуральную величину отрезка АВ и угол ψ его наклона к плоскости П1.	Задача 4.2. Определить расстояние от точки А до плоскости ∆ ВСD.
Задача 4.3. Построить проекции центра окружности, описанной вокруг треугольника АВС общего положения.	Задача 4.4. Найти расстояние между параллельными прямыми АВ и СD.