IV. Интегральный признак Коши

Признаки Даламбера и Коши не всегда являются эффективными при исследовании характера данного ряда.

Рассмотрим еще один признак, который позволяет иногда решать вопрос о сходимости ряда с положительными членами в тех случаях, когда рассмотренные выше признаки оказываются неприодными.

Этот признак основан на сравнении данного ряда с некоторым несобственным интегралом I рода от функции 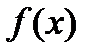, значения которой при последовательных целых значениях аргумента дают все члены этого ряда.

Теорема 6.2.10..Дан положительный ряд 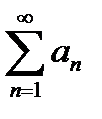(6.2.1); если существует не возрастающая непрерывная ф-ия 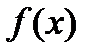, где 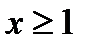, такая, ч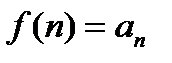то , то

1)ряд (6.2.1) сходится, если сходится несобственный интеграл 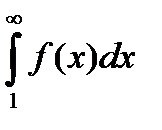; и

2)расходится, если этот интеграл расходится.

Пример 6.2.16.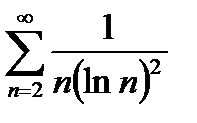

Предположим 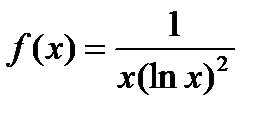- непрерывная, при 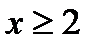функция, убывает с возрастанием х.

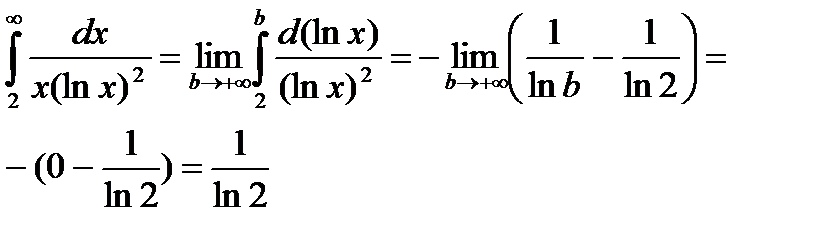
Несобственный интеграл сходится, следовательно, данный ряд сходится.

Пример 6.2.17. Исследовать на сходимость ряд 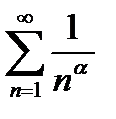, где a - любое действительное число, т. е.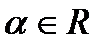

1) непосредственно видно, что при 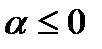член ряда 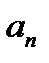стремится к нулю при неограниченном возрастании n, т. е. не выполняется даже необходимый признак сходимости ряда, и, следовательно, ряд расходится.

2)пусть теперь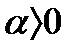

Как легко проверить, признак Даламбера и Коши вопроса о сходимости этого ряда не решают. С помощью же интегрального признака вопрос о сходимости этого ряда решается легко.

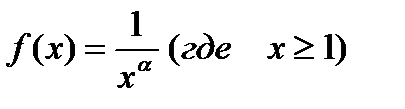- эта функция удовлетворяет всем условиям теоремы, рассмотренной выше.

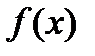( - непрерывна, положительна и убывает при )

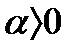Вопрос о сходимости ряда эквивалентен вопросу о сходимости несобственного интеграла

(*).

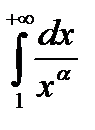При каких 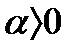существует интеграл (*)?

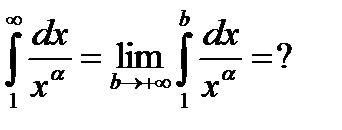
Вычислим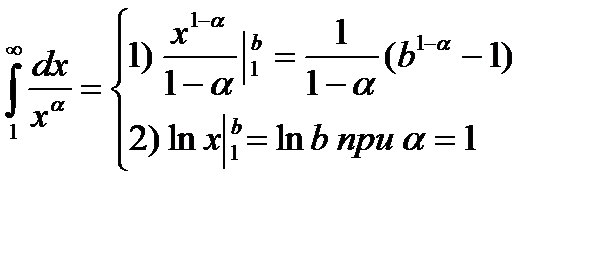

а) пусть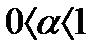

Тогда 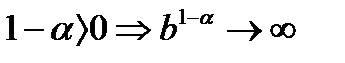при 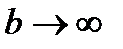и интеграл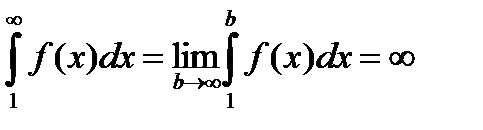

Ряд расходится.

б) пусть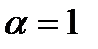

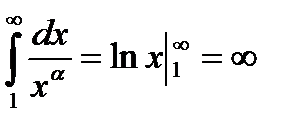- ряд расходится

в) пусть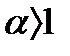

Тогда 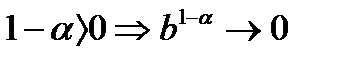при 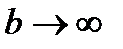Следовательно ряд сходится, т. к.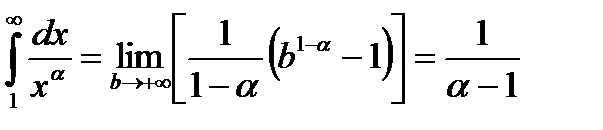

Вывод.Ряды вида 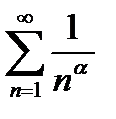1)сходятся при 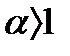и 2) расходятся при 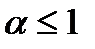, где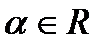

Замечание 6.2.3.При 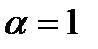ряд обращается в гармонический: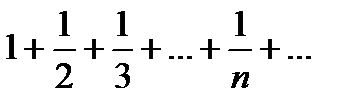

Выше мы рассмотрели теоремы сравнения, основанные на сравнении друг с другом двух рядов.

Какие же ряды используются для сравнения?

При непосредственном применении теоремы сравнения в основном пользуются рядами:

1)геометрическим рядом 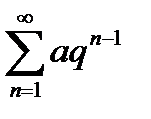(сходящимся при );

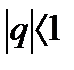2)рядами 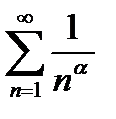(сходящимися при )

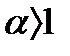Пример 6.2.18.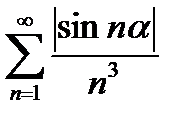

Оценим общий член ряда: 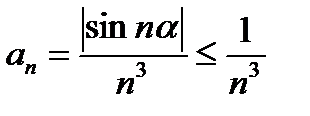, но ряд с общим членом = 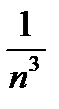сходится (a=3).

Поэтому по теореме 1 признаков сравнения данный ряд также сходится.

Пример 6.2.19.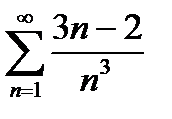

, ,

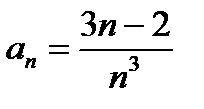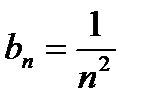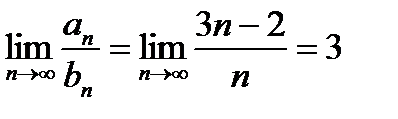
ряды сходятся или расходятся одновременно, т. к. 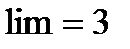. Но ряд с 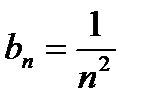- сходится. Поэтому данный ряд также сходится.