Знакочередующиеся ряды

Ряды, у которых каждые два соседних члена имеют противоположные знаки.

Обычно знакочередующийся ряд записывают в виде:

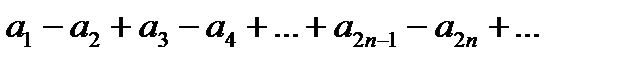
где - модули членов этого ряда

Теорема Лейбница (признак Лейбница) 6.2.11.

Если члены знакочередующегося ряда удовлетворяют условиям:

1) ;

2) , такой ряд сходится.

Пример6.2.20.Найти с точностью до 10^-3 сумму ряда

Ряд сходится, т. к. удовлетворяет всем условиям признака Лейбница.

Прежде всего надо знать, сколько слагаемых придется вычислять.

По правилу оценки погрешности вычисления надо взять столько членов, чтобы выполнялось неравенство

Тогда остаток ряда, начинающийся с этого члена, будет также меньше 10^-3.

Следовательно, решаем неравенство:

Это неравенство удовлетворяется уже при n=4.

Д-но,

Следовательно, начиная с члена , можно отбросить все члены ряда и вычислить только первые пять членов ряда.

Замечание 6.2.4. Практически удобнее находить число слагаемых так: записывают несколько первых членов ряда, а именно:

Видно, что модуль 6-го члена (по сету) меньше 10^-3.

Чтобы гарантировать требуемую точность, вычисляют каждое слагаемое с 4-мя знаками после запятой, делая при необходимости округление на 4-ом знаке.

(Все 3 цифры после запятой верные).

Замечание 6.2.5.Признак Лейбница для знакочередующихся рядов является лишь достаточным признаком сходимости, но не необходимым (т. е. ряд может сходится, хотя по признаку Лейбница не выполняется).