Числовые ряды

Основные понятия

Пусть дана бесконечная числовая последовательность: a₁, a₂, a₃,…, a_n,…

Выражение, которое получится, если все члены этой последовательности соеденить формально знаком плюс:

, (6.2.1)

называется числовым рядом (или просто рядом). Часто ряд записывают в виде 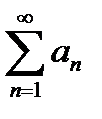, где указано, что индекс n пробегает все натуральные числа: 1, 2, 3,….

Числа a₁, a₂, a₃,…, a_n,… называются членами ряда, называют общим членом ряда (при произвольном n!!).

В арифметике и алгебре рассматривают суммы с конечным числом слагаемых. В ряде же слагаемых бесконечно много. Поэтому понятие суммы, состоящей из бесконечного числа слагаемых, требует некоторого специального определения. Что же понимают под выражением (6.2.1)?

Может оказаться, что иногда это выражение и лишнего чистого смысла.

Введем тонкое определение.

Возьмем сумму n первых членов ряда (6.2.1) и обозначим ее через S_n:

(6.2.2)

эту сумму называют n-й частичной суммой ряда (6.2.1). При этом под S₁ понимают a₁.

Давая в (6.2.2) «n» последовательных значений 1, 2, 3,…, получим последовательность частичных сумм:

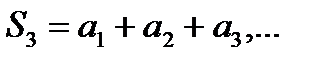
Возможны два случая:

1) либо эта последовательность имеет конечный предел

2) либо она не имеет конечного предела (стремится к ¥ или вовсе не стремится

ни к какому пределу).

Определение 6.2.1. Если последовательность частичных сумм (или иначе частичная сумма S_n) имеет конечный предел , то ряд (6.2.1) называется сходящимся, а сам этот предел называется суммой ряда.

При этом пишут: или .

Если же последовательность частичных сумм не имеет предела то ряд (6.2.1) называется расходящимся.

Расходящийся ряд не имеет суммы в том смысле как мы ее определили.

Однако в том случае когда , пишут , а также S=¥.

Пример 6.2.1. Пользуясь непосредственно определением суммы ряда, показать, что ряд сходится и найти его сумму.

Представим общий член ряда в виде суммы двух дробей:

Тогда частичную сумму S_n данного ряда можем переписать так:

В соответствии с определением надо выяснить существует ли конечный предел S_n при n®¥:

следовательно данный ряд сходится и его сумма S=1.

Решение. n=-1; A=1/3; B=-1/3.

S_n-?

Пример 6.2.2. Исследование сходимости ряда, составленного из членов геометрической прогрессии.

Рассмотрим ряд

, (6.2.3)

составленный из членов геометрической прогрессии. Часто данный ряд называют геометрическим рядом.

Выясним, при каких значениях q ряд (6.2.3) сходится.

Составим частичную сумму S_n ряда:

по формуле для суммы n первых членов геометрической прогрессии= (6.2.4)

а) если <1 (прогрессия убывающая), то 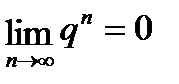, поэтому существует и

следовательно, в случае, когда <1, ряд (6.2.3) сходится и его сумма равна .

б) Если >1, то 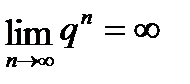, а тогда (т. к. a¹0) и

Значит, в случае, когда >1, ряд (6.2.3) расходится.

в) если q=-1, то частичная сумма S_n принимает вид:

Отсюда ясно что в этом случае S_n при n®¥ предела не имеет и ряд (6.2.3) расходится.

г) При q=1 формула (6.2.4) лишена смысла. Но ясно непосредственно, что в этом случае

Значит в случае q=1 ряд (6.2.3) также расходитс я.

Вывод. Итак геометрический ряд 1) сходится при <1 и 2) расходится ³1 (a¹0), причем при <1 имеем известную (из школьного курса математики) формулу суммы членов бесконечной убывающей геометрической прогрессии.