Понятие функционального ряда и его области сходимости

Рассмотрим ряд, членами которого являются не определенные числа (как у числового ряда), а функции:

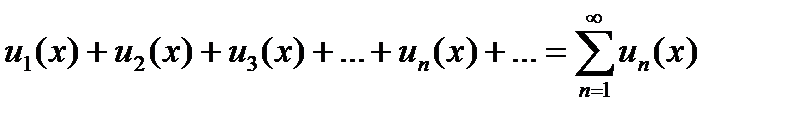(6.2.8)

Такой ряд называется функциональным рядом.

! Сходимость функционального ряда понимается следующим образом:

при каждом фиксированном значении х функции 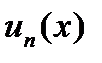принимают числовые значения и поэтому при каждом фиксированном значении х ряд (1) обращается в числовой ряд.

Причем для одних значений х ряд может быть сходящимся, а для других - расходящимся.

Определение 6.2.5. Множество всех значений х, при которых ряд (6.2.8) сходится, называется областью сходимости функционального ряда (6.2.8).

Пример 6.2.25. Найти область сходимости ряда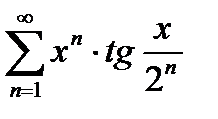

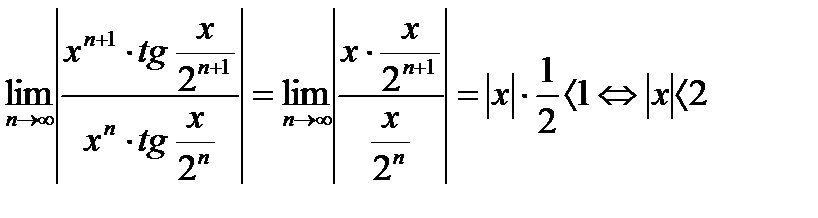
! Концы: расходятся,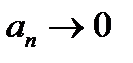

Ответ: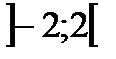

Обычно областью сходимости функционального ряда является некоторый интервал оси ОХ.

Функциональный ряд (6.2.8) называется абсолютно сходящимся в т. х₀, если в этой точке соответствующий числовой ряд 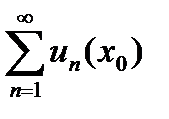сходится абсолютно.

Если ряд (6.2.8) сходится абсолютно в каждой точке данного множества, то он называется абсолютно сходящимся на этом множестве.