Уравнение плоскости в пространстве

Рассмотрим теперь простейшую поверхность - плоскость и несколько способов ее задания.

Положение плоскости в пространстве полностью определяется ее расстоянием 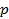от точки 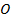(длинной перпендикуляра 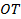, опущенного из точки 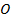на плоскость), и единичным вектором 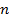, перпендикулярным плоскости и направленным от точки 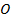к плоскости (рис.5.2). Когда точка 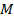движется по плоскости, то ее радиус вектор меняется так, что

. (5.1)

Это условие имеет место для всех точек плоскости и лишь для них. Но , следовательно, уравнение (5.1) может быть переписано в виде:

(5.2)

Это уравнение называется нормальным уравнением плоскости.

Переходя в уравнении (5.2) к координатам и помещая их начало в точку 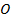, заметим, что проекции единичного вектора 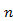на координатные оси равны его направляющим косинусам, а проекциями радиуса-вектора точки 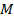служат её координаты . Выражая скалярное произведение через их координаты, получим:

. (5.3)

Уравнение (5.3) называется нормальным уравнением плоскости в канонической форме. Его степень относительно равна единице, следовательно, всякую плоскость можно задать уравнением первой степени относительно текущих координат.

Заметим, что уравнения (5.2) и (5.3) верны и тогда, когда , т.е. плоскость проходит через начало координат. В этом случае за 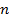можно принять любой из двух единичных векторов, перпендикулярных к плоскости (они отличаются знаком).

Покажем теперь, что всякое уравнение первой степени между тремя переменными определяет плоскость. Возьмем уравнение первой степени общего вида:

(5.4)

Будем рассматривать как проекции некоторого вектора на оси координат, а огда уравнение (5.4) может быть переписано в векторной форме в следующем виде:

(5.5)

Покажем, что уравнение (5.5) может быть приведено к нормальному виду (5.2). Рассмотрим следующие случаи.

1) Пусть . Разделим уравнение (5.5) на модуль вектора , получим: , так как . Обозначив через 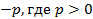, получим нормальное уравнение

2) Если , то разделим уравнение (5.5) на после чего оно примет вид: . Обозначив через 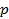, получим нормальное уравнение.

3) Если , то уравнение (5.5) можно разделить как на в первом случае мы получим 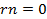, во втором - Каждое из них является нормальным уравнением.

Таким образом, уравнение (5.5) всегда может быть приведено к нормальному виду (5.2). Но нормальное уравнение определяет плоскость. Следовательно, уравнение (5.5), а значит и исходное уравнение (5.4), определяют плоскость.

Уравнение (5.4) называется общим уравнением плоскости.

Всякий вектор, отличный от нуля и перпендикулярный к плоскости, называется . Тогда, очевидно, вектор будет одним из нормальных векторов плоскости. Таким образом, коэффициенты 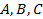при текущих координатах в уравнении (5.4) имеют простой геометрический смысл: они являются проекциями нормального вектора на оси координат. Смысл свободного члена заключается в том, что его абсолютная величина, разделенная на длину нормального вектора, равна расстоянию от плоскости до начала координат.

Если за нормаль плоскости выбран единичный вектор, направленный из начала координат перпендикулярно к данной плоскости, то уравнение (5.5) превращается в нормальное.

Чтобы привести общее уравнение плоскости к нормальному виду, надо его разделить на длину вектора взяв ее со знаком + или -, смотря по тому, будет ли свободный член отрицательным или положительным. Иными словами, для приведения общего уравнения (5.5) к нормальному виду надо умножить его на

причем знак множителя надо брать противоположным знаку свободного члена . После умножения на 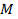уравнение (5.5) принимет вид: и совпадет с нормальным уравнением (5.3). Следовательно:

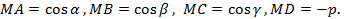(5.7)

Подставляя значение 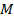из (5.6) в эти равенства, получаем:

Если то в этих формулах берется знак "+", иначе "-".

Замечание 5.1. Если два уравнения определяют одну и ту же плоскость, то соответствующие коэффициенты их пропорциональны. Действительно, будучи приведены к нормальному виду, оба эти уравнения перейдут в одно и то же нормальное уравнение. Коэффициенты каждого из них пропорциональны коэффициентам этого нормального уравнения, а потому пропорциональны и между собой.

Пример. 5.3. Уравнение плоскости привести к нормальному виду. Нормирующий множитель будет:

умножая на него данное уравнение, получим:

Для данной плоскости, следовательно, имеем:

Исследуем теперь, какое положение относительно осей координат занимает плоскость, заданная уравнением

, (5.8)

если некоторые коэффициенты этого уравнения обращаются в нуль.

Если то уравнению (5.8) удовлетворяют т.е. плоскость проходит через начало координат. Если , то

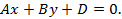(5.9)

На плоскости Oxy это уравнение задает прямую. Рассматривая же его в пространстве, мы будем иметь геометрическое место тех точек, которые проектируются на плоскость Oxy в точки указанной прямой. Таким образом, уравнение (5.9) определяет плоскость, параллельную оси Oz. Аналогично, если , то уравнение определяет плоскость, параллельную оси Oy. Наконец, если , то уравнение определяет плоскость, параллельную оси Ox.

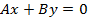Допустим теперь, что два коэффициента равны нулю,например . Уравнение определяет плоскость, проходящую через начало координат параллельно оси Oz, т.е. это будет плоскость, проходящая через ось Oz. Аналогично уравнение вида определяет плоскость, проходящую через ось Oy, а уравнение определяет плоскость, проходящую через ось Ox.

Если равны нулю два коэффициента при текущих координатах, например то уравнение определяет плоскость, параллельную оси Ox и оси Oy, т.е. плоскость, параллельную плоскости координат Oxy. Также уравнения и определяют плоскости, параллельные соответственно Oxz и Oyz.

Если, наконец, три коэффициента равны нулю, например 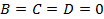, то уравнение определяет плоскость координат Oyz. Также уравнения и определяют соответственно плоскости координат Oxz и Oxy.

Приведем еще несколько форм задания уравнения плоскости.

Уравнение плоскости в отрезках. Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Ее уравнение можно записать в виде

, (5.10)

где ни один из коэффициентов не равен нулю. Обозначим через 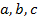величины отрезков, отсекаемых плоскостью на осях координат (рис.5.3). Так как точка ) лежит на плоскости, то ее координаты удовлетворяют уравнению (5.10), тогда 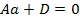или

Аналогично, используя точки получим:

0

x

y

z

P

R

Q

x

y

z

M

N

r

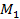
Рис. 5.3. Уравнение плоскости в отрезках.

Рис.5.4. Уравнение плоскости, через точку.

Подставляя найденные значения 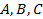в уравнение (5.10), получим:

Сокращая на , которое в силу предположения не равно нулю, найдем: , или

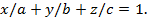
Это и есть искомое уравнение плоскости в отрезках.

Пример 5.4. Уравнение плоскости написать в отрезках. Полагая в данном уравнении найдем . Аналогично, полагая . Следовательно, искомое уравнение в отрезах будет .

Уравнение плоскости, проходящей через точку . Найдем уравнение плоскости, проходящей через точку M с радиус-вектором (a;b;c) и перпендикулярной вектору . Обозначим эту плоскость (рис.5.4).

Проведем радиус-вектор в произвольную точку 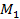этой плоскости. Тогда вектор или , как лежащий в плоскости P, будет перпендикулярен вектору N. Поэтому их скалярное произведение равно нулю:

(5.11)

Это равенство есть условие того, что точка 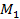лежит в плоскости . Оно справедливо для всех точек этой плоскости и нарушается только тогда, когда точка 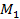оказывается вне плоскости Выражая скалярное произведение векторов через координаты сомножителей, получим уравнение плоскости, проходящей через заданную точку, в координатной форме:

. (5.12)

Изменяя значения 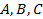, мы будем получать различные плоскости, проходящие через данную точку 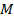. Таким образом, уравнение (5.12) при любых значениях коэффициентов 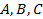задает плоскость, проходящую через точку ).

Пример 5.5. Составить уравнение плоскости, проходящей через точку перпендикулярно данному вектору Уравнение искомой плоскости:

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой. Рассмотрим три точки, не лежащие на одной прямой. Обозначим их радиусы-векторы через а радиус-вектор текущей точки 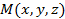через . Векторы

, лежат в одной плоскости, следовательно, они компланарные и их смешанное произведение равно нулю:

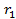( - )()()=0. (5.13)

Это и есть уравнение плоскости, проходящей через три заданные точки в векторной форме. Переходя к координатам, получаем:

=0

где

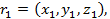
Если три данные точки лежат на одной прямой, то векторы , коллинеарны. Поэтому соответствующие элементы двух нижних строк определителя пропорциональны и определитель равен нулю. Следовательно, уравнение (5.14) обращается в тождество при любых значениях . Геометрически это означает, что через каждую точку пространства проходит плоскость, в которой лежат три данные точки.

Пример 5.6. Найти уравнение плоскости, проходящей через точки . Используем уравнение (5.14):

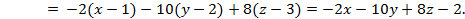
Отсюда получаем искомое уравнение: .