Основные задачи о положении прямой

Рассмотрим теперь некоторые задачи о положении прямой.

Углом между прямыми в пространстве называется любой из углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным прямым. При этом условимся брать угол в пределах от 0 до .

Рассмотрим уравнения двух прямых:

очевидно, за угол 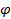между ними можно принять угол между их направляющими векторами и или угол, дополняющий его до . Поэтому

в формуле (5.27) можно брать любой знак, что соответствует выбору одного из двух различных углов между данными прямыми.

Пример 5.12. Найти угол между прямыми /(-1). Для первой прямой направляющие коэффициенты будут: , , , а для второй: 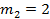, , . Следовательно:

Откуда или .

Для перпендикулярных прямых =0, и из формулы (5.27) мы получаем условие перпендикулярности двух прямых:

.

Условием параллельности прямых будет выполнение равенств:

.

Это условие можно получить, заметив, что направляющие векторы прямых коллинеарны.

Рассмотрим задачу о нахождении уравнений прямой, проходящей через две заданные точки и . Будем искать эти уравнения в канонической форме.

Для решения задачи достаточно знать координаты одной из точек, лежащих на прямой, и направляющий вектор. Возьмем, например, точку 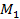. За направляющий же вектор прямой примем вектор . Проекции его на координатные оси равны

.

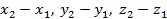Уравнения искомой прямой примут вид: