Парабола. Парабола есть геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой

Парабола есть геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что данная точка не лежит на этой директрисе).

Чтобы составить уравнение параболы, примем за ось Ox прямую, проходящую через фокус 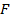перпендикулярно к директрисе, и будем считать ее направленной от директрисы к фокусу; за начало координат возьмем середину 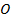отрезка от точки 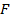до директрисы, длину которого обозначим через 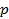(рис.4.15). Величину 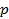называют параметром параболы. Координаты фокуса F 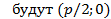. Обозначим через 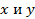координаты произвольной точки 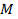параболы. Тогда координаты точки 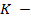основания перпендикуляра, опущенного из 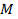на директрису, будут 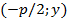. Так как по определению , то, применяя формулу расстояния между двумя точками, получим уравнение параболы:

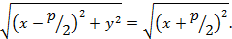
Возведем обе его части в квадрат:

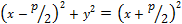или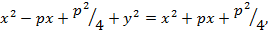

откуда

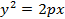. (4.37)

Полученное уравнение параболы называется каноническим.

y

K

p

M

F

x

Рис.4.15. Парабола.

Уравнению (4.37) удовлетворяют координаты любой точки на параболе и, как можно показать, никакой другой точки. Парабола (4.37) изображена на рис.4.15. Она имеет одну ось симметрии. Точка ее пересечения с этой осью называется вершиной. Для параболы (4.37), вершиной является начало координат.

Пусть - расстояние от произвольной точки 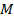параболы до ее фокуса, а 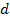- расстояние от 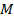до директрисы. Мы имеем: 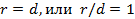. Поэтому эксцентриситет параболы принимают равным единице. Уравнение директрисы параболы будет: 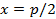, если оси координат выбраны так, как это показано на рис.4.15.

Если ветви параболы направлены влево, то ее уравнением будет 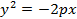, при этом ее фокусом является точка 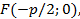а директриса задается уравнением 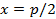. Если вершиной параболы является точка 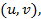а ее ось симметрии параллельна оси абсцисс, то уравнением параболы будет

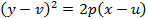или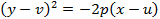

в зависимости от uтого, куда направлены ее ветви. Если же ось симметрии параллельна оси ординат, то парабола задается уравнением

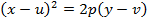или .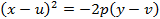

Рассмотрим, например, первое из этих уравнений. Имеем: 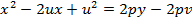, откуда , где

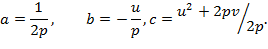
Таким образом, мы получаем хорошо знакомое со школы уравнение параболы.