 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Классификация кривых второго порядка
|
|
Мы видели, что все три рассмотренные линии - эллипс, гипербола, парабола - в декартовой системе координат могут быть представлены уравнениями второй степени. Можно показать, что любому уравнению второй степени с двумя переменными в декартовой системы координат соответствует одна из указанных кривых.
Приведем несколько замечаний по поводу преобразования декартовой системы координат на плоскости.
| a |
| b |
| x |
| y |

|
| X |
| Y |
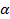
|
| x |
| y |
| X |
| Y |
| M |

|
| p |
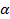
|
Рис.4.16. Системы координат
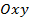 и и  . .
|
| Рис. 4.17. Поворот осей. |
Пусть даны две декартовы системы координат Oxy и O'XY (рис.4.16). Чтобы задать положение новой системы O'XY относительно старой Oxy, надо знать координаты a и b начала O' новой системы и угол 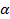 между осями Ox и O'X.
между осями Ox и O'X.
Через x и y будем обозначать координаты точки M в старой системе, а через X и Y - в новой. Требуется выразить старые координаты x и y через новые X и Y и постоянные a, b и  .
.
Рассмотрим два частных случая.
1. Начало координат сдвигается, а направления осей сохраняется ( ). Этот случай нами рассматривался в 3.1.
). Этот случай нами рассматривался в 3.1.
2. Меняются направления осей, начало же координат остается неизменным (рис.4.17).
Пусть 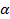 есть угол между осями Ox и OX. Как и раньше x, y - координаты точки M в старой системе, X, Y - в новой.
есть угол между осями Ox и OX. Как и раньше x, y - координаты точки M в старой системе, X, Y - в новой.
Рассмотрим векторы  . Их сумма равна вектору
. Их сумма равна вектору  Следовательно, проекция их суммы на ось Ox, равная сумме
Следовательно, проекция их суммы на ось Ox, равная сумме
 ,
,
но
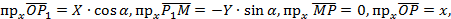
тогда
 . (4.38)
. (4.38)
Аналогично, проектируя рассматриваемые векторы на ось 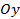 , получим, что
, получим, что
 . (4.39)
. (4.39)
Легко видеть, что при одновременном сдвиге начала координат и повороте координатных осей связь между старыми и новыми координатами точки M выражается формулами:


Вернемся теперь к уравнению второй степени
 (4.40)
(4.40)
Очевидно, что замена переменных в этом уравнении не изменяет графика кривой, которую оно задает, но при линейном преобразовании переменных изменяется система координат на плоскости (происходит сдвиг начала координат, изменение масштабов по осям, изменение направлений осей).
Прежде всего покажем, что уравнение (4.40) можно преобразовать так, что в нем не будет содержаться член с произведением переменных. Для этого необходимо повернуть оси на некоторый угол 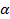 , величину которого мы определим позже. Итак, пусть
, величину которого мы определим позже. Итак, пусть  . Положим
. Положим
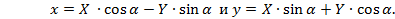
Подставим эти выражения в уравнение (4.40):


Приводя подобные члены, получим наше уравнение в новых координатах:

где 

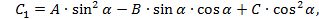

Выберем теперь 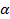 так, чтобы коэффициент
так, чтобы коэффициент 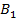 равнялся нулю, т.е. чтобы выполнялось:
равнялся нулю, т.е. чтобы выполнялось:  или
или

Так как  (иначе
(иначе 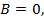 что противоречит предположению), то из последнего уравнения получаем, что
что противоречит предположению), то из последнего уравнения получаем, что 
Зная требуемое значение котангенса2, мы можем определить значения  и
и  , необходимые нам для перехода к новым координатам, для этого можно воспользоваться формулами:
, необходимые нам для перехода к новым координатам, для этого можно воспользоваться формулами:

.
В результате описанных преобразований наше уравнение (4.40) примет вид:
 (4.41)
(4.41)
Поскольку любое уравнение (4.40) с  может быть приведено к форме, не содержащей произведения переменных, то будем считать, что уравнение (4.40) имеет вид:
может быть приведено к форме, не содержащей произведения переменных, то будем считать, что уравнение (4.40) имеет вид:
 (4.42)
(4.42)
Преобразуем его левую часть следующим образом, выделяя полные квадраты (предполагая, что  и
и  ):
):


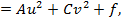
где

В итоге уравнение (4.42) в предположении, что  и
и  преобразуется в уравнение
преобразуется в уравнение
 (4.43)
(4.43)
Будем предполагать, что  , иначе умножим обе части уравнения на (-1).
, иначе умножим обе части уравнения на (-1).
Если  , то мы получаем из уравнения (4.43) линейные уравнения:
, то мы получаем из уравнения (4.43) линейные уравнения:

Аналогично в случае, когда  .
.
Если 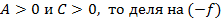 , мы получаем уравнение эллипса.
, мы получаем уравнение эллипса.
Если  получаем уравнение гиперболы, аналогично в случае, когда
получаем уравнение гиперболы, аналогично в случае, когда  .
.
Если  и
и  , то уравнение задает мнимое геометрическое место точек (если еще и
, то уравнение задает мнимое геометрическое место точек (если еще и  , то уравнение задает единственную точку (0,0)).
, то уравнение задает единственную точку (0,0)).
Пусть теперь один из коэффициентов 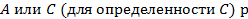 авен нулю. Тогда уравнение (4.42) имеет вид:
авен нулю. Тогда уравнение (4.42) имеет вид:
 . (4.44)
. (4.44)
Если  то уравнение
то уравнение  задает пару прямых
задает пару прямых

где e  его корни.
его корни.
Если  , то разделив обе части уравнения (4.44) на
, то разделив обе части уравнения (4.44) на 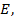 мы получим
мы получим

обозначив  придем к уравнению
придем к уравнению  .
.
Преобразуем его к виду

или

Перенесем начало координат в точку

.
Полагая

получим уравнение 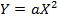 . Это есть уравнение параболы.
. Это есть уравнение параболы.
Рассмотренными случаями полностью исчерпываются все возможные ситуации с уравнением (4.42). Тем самым мы показали, что уравнение второй степени задает одну из трех кривых: эллипс, гиперболу, параболу. В некоторых случаях оно вырождается в линейные уравнения, но тогда оно перестает быть уравнением второй степени с двумя переменными.
Дата публикования: 2014-11-02; Прочитано: 370 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
