Задачи на взаимное расположение прямой и плоскости

Пусть прямая и плоскость заданы уравнениями::

(5.28)

Найдем угол между ними. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Найдем синус этого угла 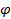, при этом в дальнейшем будем считать, что , потому что синусы смежных углов равны. Угол будет углом между прямой и перпендикуляром к плоскости. Его косинус найдем по координатам 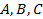нормали к плоскости и координатам направляющего вектора данной прямой; так как , то мы получим

Числитель берется по абсолютной величине, так как

В случае параллельности прямой и плоскости: угол между ними равен нулю, следовательно, , и формула (5.29) дает необходимое и достаточное условие параллельности: .

Условие перпендикулярности прямой и плоскости 0совпадает с условием параллельности этой прямой и перпендикуляра к плоскости: .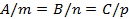

Найдем теперь координаты точки пересечения прямой с плоскостью, для чего надо совместно решить уравнения (5.28).

Так как все три отношения в уравнениях прямой равны, то мы можем эти уравнения записать в виде:

где 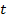- неизвестный параметр. В результате мы получим четыре уравнения первой степени с четырьмя неизвестными:

Из первых трех уравнений находим:

(5.30)

Подставляя эти значения в четвертое уравнение, получаем:

или

,

откуда находим:

.

Подставляя найденное значение 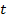в формулы (5.30), найдем координаты искомой точки. Если , то 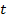имеет определенное конечное значение; следовательно, в этом случае прямая пересекает плоскость в одной точке.

В случае, когда и прямая параллельна плоскости (в силу первого равенства), а точка через которую проходит прямая, лежит вне плоскости, следовательно, прямая не имеет общих точек с плоскостью.

Если то прямая параллельна данной плоскости и проходит через точку лежащую в этой плоскости (в силу второго равенства), следовательно прямая вся лежит в данной плоскости.

Рассмотрим две прямые, заданные уравнениями:

Обозначим направляющий вектор первой из них через , второй - через . Как видно из уравнений прямых, первая из них проходит через точку с радиусом-вектором 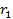, вторая - через точку с радиусом-вектором 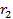. Рассмотрим вектор , его проекциями будут: . Из геометрических соображений ясно, что данные прямые лежат в одной плоскости в том и только том случае, если три вектора компланарны. Следовательно, искомое условие принадлежности двух прямых плоскости заключается в равенстве нулю смешанного произведения этих трех векторов:

или, в проекциях:

.