Уравнения прямой в пространстве

Положение прямой в пространстве будет вполне определено, если на прямой задать некоторую точку при помощи ее радиуса-вектора и вектор (отличный от нулевого), параллельный рассматриваемой прямой (рис.5.7). Этот вектор назовем направляющим вектором прямой. Переменной точке M прямой соответствует ее радиус-вектор 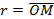, и из рис.5.7 мы видим, что

(5.21а)

0

S

M

r

Рис.5.7. Векторное уравнение прямой.

Вектор параллелен вектору , значит , где может принимать любые значения в зависимости от положения точки 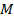на прямой. Равенство (5.21а) можно переписать так:

, (5.21)

причем 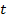играет роль переменного параметра. Уравнение (5.21) называется векторным уравнением прямой.

Обозначим декартовы координаты точки относительно системы с началом в точке O через 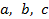, текущие координаты точки 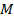- через Проекции вектора - через 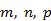. Написав уравнение (5.21) в проекциях, получим параметрические уравнения прямой.

. (5.22)

Заметим, что при единичном векторе коэффициенты становятся косинусами углов 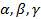, образованными данной прямой с осями координат. В этом случае уравнения (5.21) и (5.22) принимают вид:

Параметр 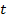здесь имеет простой геометрический смысл: 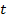обозначает расстояние от переменной точки 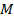до точки , взятое со знаком + или - в зависимости от того, будет ли направление вектора одинаково или нет с направлением вектора .

Очевидно, что отсюда

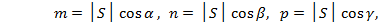(5.23)

т.е. пропорциональны направляющим косинусам прямой, причем коэффициентом пропорциональности служит длина вектора :

Таким образом, мы получаем:

Вместо параметрических уравнений, прямую обычно определяют посредством системы двух уравнений первой степени между текущими координатами. Эти уравнения получаются из параметрических путем исключения параметра 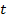. Так, из уравнений (5.22) находим:

или

. (5.24)

Уравнения (5.24) называются каноническими уравнениями прямой. В частности, при уравнения (5.24) примут вид:

.

Система двух уравнений (5.24) представляет прямую как пересечение двух плоскостей, задаваемых уравнениями:

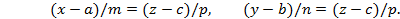
Заметим, что в канонических уравнениях все коэффициенты не могут обратиться в нуль одновременно, так как . Но некоторые из них могут быть равны нулю. В этом случае формула (5.24) принимается условно.

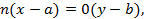Пусть, например, Тогда будем иметь: то есть . Заметим, что равенства геометрически означают одно и тоже: первое из них показывает, что прямая перпендикулярна к оси абсцисс, а второе, что прямая лежит в плоскости, перпендикулярной к оси абсцисс.

Пусть в канонических уравнениях прямой

коэффициент 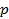отличен от нуля, т.е. прямая не параллельна плоскости Oxy. Запишем эти уравнения раздельно в таком виде:

(5.25)

Каждое из них в отдельности задает плоскость, причем первая из них параллельна оси ординат, а вторая - оси абсцисс.

Таким образом, представляя прямую уравнениями (5.25), мы рассматриваем ее как пересечение двух плоскостей, проектирующих эту прямую на плоскости координат Oxz и Oyz.

Если бы направляющий коэффициент 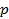был равен 0, то обязательно, хотя бы один из двух других коэффициентов, например , был бы отличен от нуля, т.е. прямая не была бы параллельна плоскости Oyz. В этом случае мы могли бы выразить прямую уравнениями плоскостей, проектирующих ее на координатные плоскости Oxy и Oxz, записав уравнения (5.24) в виде

Таким образом, любая прямая может быть выражена уравнениями двух плоскостей, проходящих через нее и проектирующих ее на координатные плоскости.

Через каждую прямую проходит бесконечное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно, представляют уравнения этой прямой.

Вообще всякие две не параллельные между собой плоскости с уравнениями

определяют прямую, являющуюся их пересечением.

Уравнения (5.26), рассматриваемые совместно, называются общими уравнениями прямой.

От общих уравнений прямой можно перейти к ее каноническим уравнениям. Для этого надо знать какую-нибудь точку прямой и ее направляющий вектор. Координаты точки легко находятся из данной системы уравнений, одну из координат можно взять произвольно и затем надо решить систему двух уравнений с двумя неизвестными. Направляющий вектор прямой перпендикулярен к обоим нормалям рассматриваемых плоскостей. Поэтому в качестве него можно взять вектор, направленный по линии пересечения плоскостей, являющийся векторным произведением этих нормалей.

Пример 5.11. Написать канонические уравнения прямой . Выберем произвольно одну из координат. Пусть, например, . Тогда получим систему: , откуда . Итак, точка (2;0;1), лежит на нашей прямой. Найдем теперь векторное произведение векторов (2,-3,1) и (3;1;-2), получим направляющий вектор прямой (5;7;11). Поэтому канонические уравнения будут:

.