Постановка задачи. Пусть, изучая функциональную зависимость переменной от , мы произвели ряд измерений величин ,

Пусть, изучая функциональную зависимость переменной 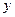от 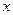, мы произвели ряд измерений величин 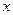, 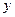и получили таблицу 2.1 значений этих переменных. Если аналитическое выражение функции неизвестно или сложно, то возникает практически важная задача [1,2]: найти эмпирическую формулу 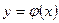,значения которой при 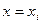возможно мало отличались бы от опытных данных .

Таблица 2.1

				...		...
				...		...

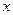
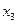
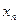
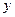
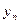
В такой постановке эта задача имеет много решений. Поэтому вводят дополнительное условие, чтобы эмпирические формулы были наиболее простыми, например, из класса линейных, степенных, показательных, логарифмических и др. функций.

Геометрически задача построения эмпирической формулы сводится к проведению кривой Г (рисунок 1) «возможно ближе» примыкающей к данной системе точек .

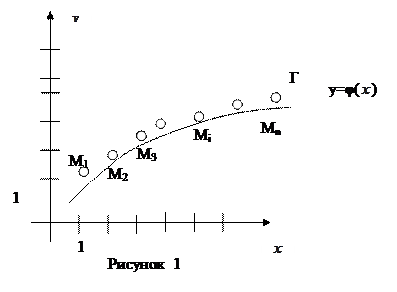
Если вид эмпирической формулы подобран, остаётся лишь найти наилучшие значения параметров.

Задача построения эмпирической формулы состоит из трех этапов:

Подбор вида эмпирической формулы.

Определение наилучших значений параметров.

Выявление «близости» полученной эмпирической формулы к табличным данным.