Нелинейные эмпирические формулы и аналитические критерии их существования

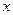Предположим, что точки не располагаются на прямой линии. Это значит, что зависимость между переменными и 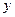нелинейная. Во многих случаях можно подобрать эмпирические формулы из класса показательных функций , степенных 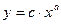, логарифмических 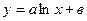. Для существования конкретной нелинейной зависимости должна существовать определенная зависимость между табличными данными.

Допустим, что зависимость между переменным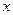и и 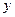описывается степенной функцией 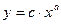. Предполагая 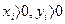, вычислим среднее геометрическое 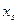значений и 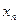, т.е. 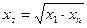, тогда

Таким образом, для существования степенной зависимости между переменным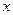и и 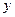необходимо, чтобы среднему геометрическому 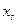значений аргумента 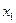и , соответствовало среднее геометрическое значений функции и .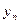

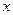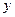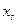Если зависимость между переменными и описывается показательной функцией , то должны выполнятся другие условия для табличных данных. Найдем среднее арифметическое значений аргумента 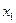и , т.е. 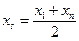, тогда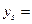

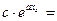
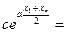
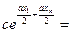
Таким образом, табличные данные могут быть описаны показательной функцией, если среднему арифметическому 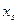значений аргумента и 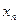соответствует среднее геометрическое значений функций и .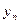

Пусть эмпирическая формула имеет вид: 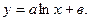Вычислим среднее геометрическое 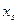значений аргумента и 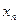, т.е. 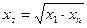, тогда .

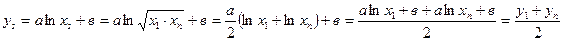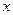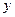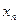Таким образом, для существования логарифмической зависимости между переменными и нужно, чтобы среднему геометрическому значений аргумента и , соответствовало среднее арифметическое значений функций и 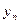. Все полученные соответствия сведём в таблицу 2.8.

Таблица 2.8

		Вид эмпирической формулы

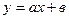
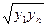
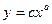
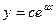
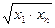
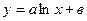
2.6 Метод выравнивания нелинейных эмпирических формул

Допустим, что для табличных данных подобрана одна из нелинейных эмпирических формул или 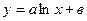. Суть метода выравнивания заключается в том, заменой переменных нелинейную эмпирическую формулу можно свести к линейной.

Пусть нами установлено, что результаты эксперимента описываются степенной функцией 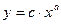. Полагая все значения 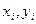, с положительными, прологарифмируем обе части этого равенства 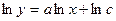. Обозначив через получим , а это означает, что новая система точек 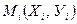, в новой системе координат располагается на прямой , где 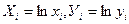. Аналогично поступаем с другими эмпирическими формулами.

В таблице 2.9 приведена замена переменных, позволяющая рассматриваемые нелинейные эмпирические формулы свести к линейной зависимости в новой системе координат.

Таблица 2.9

Эмпирическая формула	Вид замены переменной	Линейная зависимость

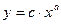
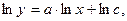
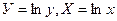
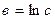
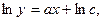
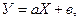
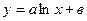
После того, как нелинейная эмпирическая формула сведена к линейной и установлено, что система точек 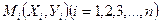располагается приблизительно на прямой линии, параметры 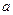и можно найти методом выбранных точек или методом наименьших квадратов.