Связь конечных разностей со степенью многочлена

Пример 9. Составить таблицу 1.10 конечных разностей для линейной функции 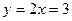на отрезке 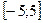с шагом .

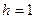Таблица 1.10

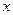
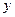
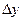
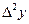
-5	-7
-4	-5
-3	-3
-2	-1
-1

Как видим, для многочлена первой степени конечные разности второго порядка, составленные для равноотстоящих значений аргумента равны нулю.

Пример 10. Составить таблицу 1.11 конечных разностей для квадратичной функции 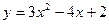на отрезке 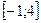с шагом .

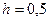Таблица 1.11

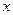
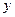
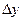
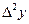
-1	9,00	-4,25	1,50
-0,5	4,75	-2,75	1,50
	2,00	-1,25	1,50
0,5	0,75	0,25	1,50
	1,00	1,75	1,50
1,5	2,75	3,25	1,50
	6,00	4,75	1,50
2,5	10,75	6,25	1,50
	17,00	7,75	1,50
3,5	24,75	9,25
	34,00

Мы видим, что конечные разности третьего порядка равны нулю. Справедлив общий вывод. Для многочленов степени 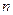все конечные разности порядка, образованные для равностоящих значений аргумента, равны нулю. Справедливо и обратное утверждение. Если конечные разности функции, образованные для равностоящих значений аргумента нули, то функция есть многочлен степени .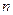

Этот вывод позволяет по конечным разностям судить о близости таблично заданной функции к многочлену какой-то степени.

Пример11. Составить конечные разности для функции, заданной таблицей 1.12 и выяснить, к многочлену какой степени функция близка.

Таблица1.12

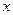
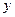
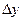
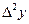
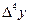
0,30	1,03076	-0,0405	0,0044	-0,0008	0,0001
0,35	0,9971	-0,0361	0,0036	-0,0007	0,0001
0,40	0,9610	-0,0397	0,0029	-0,0006	0,0000
0,45	0,9213	-0,0426	0,0023	-0,0006	0,0000
0,50	0,8787	-0,0449	0,0017	-0,0006	0,0000
0,55	0,8338	-0,0466	0,0011	-0,0006
0,60	0,7872	-0,0477	0,0005
0,65	0,7395	-0,0482
0,70	0,6913

Конечные разности четвёртого порядка почти нули, значит, функция ведёт себя как многочлен третьей степени на рассматриваемом промежутке.