Конечные разности

До сих пор не делалось никаких предположений о заданных значениях аргумента. Теперь предположим, что рассматриваемые значения аргумента являются равноотстоящими, т.е. дана таблица 1.1, где 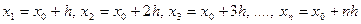, h – шаг таблицы.

Таблица 1.1

					…
					…

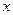
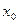
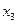
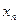
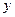
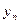
Построение интерполяционных многочленов в этом случае упрощается. Предварительно введем понятие конечных разностей.

Конечными разностями первого порядка называются разности .

Конечными разностями второго порядка называются разности .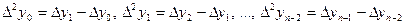

В общем случае конечные разности k-го порядка

.

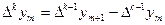Последовательно получаемые конечные разности записывают в таблицу 1.8

Таблица 1.8

				...
				...
				...
				...
…	...	...	...	...

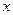
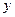
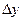
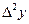
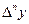
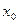
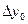
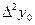
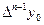
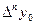
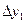
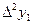
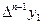
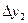
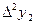
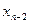
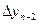
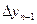
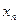
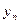
Пример 8. Построить таблицу 1.9 конечных разностей для функции на отрезке 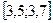с шагом .

Таблица 1.9

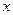
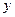
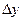
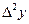
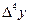
3,50	33,115	1,698	0,087	0,0005	-0,002
3,55	34,813	1,785	0,092	0,003
3,60	36,598	1,877	0,095
3,65	38,475	1,972
3,70	40,447