 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 1 Приближение функций
|
|
Интерполирование функций
Пусть 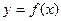 - некоторая функция, для которой известна таблица 1.1 ее значений.
- некоторая функция, для которой известна таблица 1.1 ее значений.
Таблица 1.1
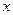
| 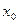
| 
| 
| 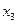
| … | 
| 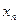
|
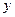
| 
| 
| 
| 
| … | 
| 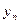
|
Требуется найти многочлен (полином)
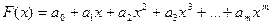 , (1.1)
, (1.1)
который в точках 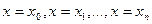 принимал бы те же значения
принимал бы те же значения 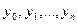 , т.е. удовлетворял условию
, т.е. удовлетворял условию
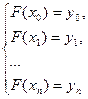 (1.2)
(1.2)
Многочлен  , удовлетворяющий условиям (1.2), называется интерполяционным многочленом. В этом случае функцию
, удовлетворяющий условиям (1.2), называется интерполяционным многочленом. В этом случае функцию 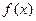 и многочлен
и многочлен  считают близкими, так как они совпадают на заданной системе точек
считают близкими, так как они совпадают на заданной системе точек 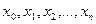 . Точки
. Точки 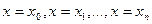 называются узлами интерполирования.
называются узлами интерполирования.
Как для данной системы точек построить интерполяционный многочлен  ?
?
Можно считать степень многочлена 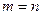 и определить коэффициенты
и определить коэффициенты 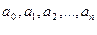 из системы
из системы 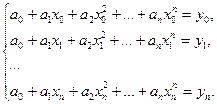 (1.2
(1.2  )
)
Если значения 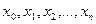 отличны друг от друга, тогда система (1.2
отличны друг от друга, тогда система (1.2  ) имеет единственное решение
) имеет единственное решение 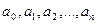 и интерполяционный многочлен
и интерполяционный многочлен 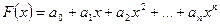 будет найден.
будет найден.
Пример 1. Построить интерполяционный многочлен 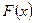 , совпадающий с функцией
, совпадающий с функцией 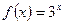 в точках
в точках 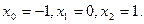
Решение. Составим таблицу (1.2) значений функции 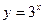 в узлах интерполирования.
в узлах интерполирования.
Таблица 1.2
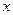
| 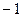
| 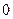
| 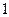
|

| 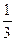
| 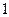
| 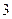
|
Так как 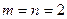 , то многочлен ищем в виде
, то многочлен ищем в виде 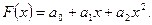
Для определения коэффициентов составляем систему (1.2  )
)
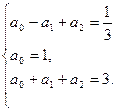
Отсюда имеем 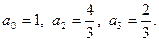
Интерполяционный многочлен примет вид 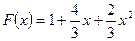 и считаем, что
и считаем, что 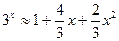
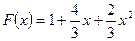 при
при 
Следует заметить, что значения функций 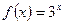 и
и 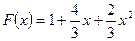 совпадают лишь в трёх точках, а в остальных точках их значения отличаются. Например,
совпадают лишь в трёх точках, а в остальных точках их значения отличаются. Например, 
Графическая иллюстрация решённой задачи интерполирования показана на рисунке 1.1.
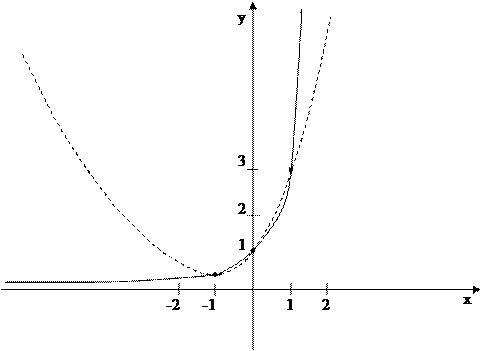
Рис. 1.1
Основная идея применения интерполяционных формул состоит в том, что функция 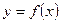 , для которой известна таблица её значений, заменяется интерполяционным многочленом, который рассматривается как приближённое аналитическое выражение для функции
, для которой известна таблица её значений, заменяется интерполяционным многочленом, который рассматривается как приближённое аналитическое выражение для функции  . Такая замена может потребоваться тогда, когда аналитическое выражение для
. Такая замена может потребоваться тогда, когда аналитическое выражение для  неизвестно или является слишком сложным.
неизвестно или является слишком сложным.
Пример 2. Для функции 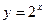 построить интерполяционный многочлен, совпадающий в точках
построить интерполяционный многочлен, совпадающий в точках 
Ответ. 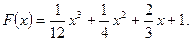
Дата публикования: 2014-11-02; Прочитано: 488 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
