 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показникові рівняння та нерівності
|
|
Показниковими називаються рівняння, у яких невідоме міститься в показнику степеня при постійних основах.
Наприклад. Рівняння  ;
;  є показниковими.
є показниковими.
Найпростішим показниковим рівнянням є рівняння  , де
, де  .
.
Оскільки множина значень функції  - множина додатних чисел, то рівняння
- множина додатних чисел, то рівняння  :
:
1) має один корінь, якщо  ;
;
2) не має коренів, якщо  .
.
Для того, щоб розв’язати рівняння  , де
, де  , треба
, треба 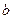 подати у вигляді
подати у вигляді  , тоді будемо мати
, тоді будемо мати  , звідси
, звідси  .
.
Наприклад.


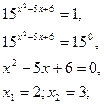

164. Розв’язати рівняння:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9) 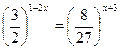 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19)  ; 20)
; 20)  .
.
165. Розв’язати рівняння:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 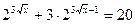 ;
;
5)  ; 6)
; 6)  ;
;
166. Розв’язати рівняння:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  .
.
167. Розв’язати нерівності:
1)  ; 2)
; 2)  ;
;
3) 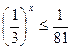 ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 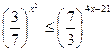 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ; 16)
; 16)  .
.
До змiсту
Дата публикования: 2014-11-04; Прочитано: 454 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
