 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Логарифмічна функція та її властивості
|
|
Оскільки показникова функція 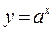 (
( ) є монотонно зростаючою при
) є монотонно зростаючою при  і монотонно спадною при
і монотонно спадною при  , то вона має зворотну функцію. Щоб знайти цю зворотну функцію потрібно зі співвідношення
, то вона має зворотну функцію. Щоб знайти цю зворотну функцію потрібно зі співвідношення 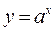 виразити
виразити 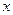 через
через 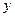 (тобто
(тобто  ), а потім поміняти позначення
), а потім поміняти позначення 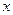 на
на 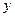 ,
, 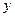 на
на 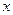 ; тоді дістанемо
; тоді дістанемо  .
.
Функція  (
( ) називається логарифмічною.
) називається логарифмічною.
Таким чином, показникова і логарифмічна функції при тій самій основі є взаємно оберненими функціями.
Графік функції  при
при  виглядає так, як показано на рисунку 29
виглядає так, як показано на рисунку 29
 Рис. 29
Рис. 29
Властивості функції  при
при  :
:
1) область визначення функції – проміжок  , тобто
, тобто  ;
;
2) область значень функції – уся числова пряма, тобто  ;
;
3) функція не є ні парною, ні непарною;
4) функція зростає при  , тобто
, тобто 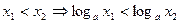 ;
;
5) при  значення функції дорівнює 0, тобто
значення функції дорівнює 0, тобто  ;
;
6) якщо  , то
, то 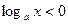 ;
;
7) якщо  , то
, то  .
.
Графік функції  при
при  виглядає так, як показано на рисунку 30
виглядає так, як показано на рисунку 30
 Рис. 30
Рис. 30
Властивості функції  при
при  :
:
1) область визначення функції – проміжок  , тобто
, тобто  ;
;
2) область значень функції – уся числова пряма, тобто  ;
;
3) функція не є ні парною, ні непарною;
4) функція спадає при  , тобто
, тобто  ;
;
5) при  значення функції дорівнює 0, тобто
значення функції дорівнює 0, тобто  ;
;
6) якщо  , то
, то  ;
;
7) якщо  , то
, то 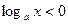 .
.
156. Знайти область визначення функції:
1)  ; 2)
; 2) 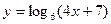 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
157. Порівняти з нулем:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 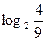 ;
;
7)  ; 8)
; 8)  .
.
158. Порівняти 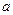 і
і 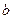 , якщо:
, якщо:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
159. Порівняти з одиницею основу логарифма, якщо:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
160. Побудувати графіки функцій:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9) 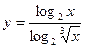 ; 10)
; 10)  .
.
До змiсту
Дата публикования: 2014-11-04; Прочитано: 536 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
