Неперервність функції

135. Використовуючи графіки функцій (рис. 23) указати точки розриву функцій і назвати проміжки неперервності:

Рис. 23

Функція називається неперервною в точці 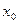, якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці .

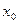Отже, функція 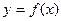в точці 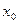буде неперервною тоді і тільки тоді, коли виконуються такі умови:

1) функція 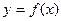визначена в точці ;

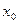2) для функції існує границя ;

3) границя функції в точці 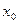дорівнює значенню функції в цій точці: .

Якщо функція 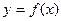неперервна в кожній точці деякого проміжку, то її називають неперервною на проміжку.

Запам’ятайте:

1) Многочлен - неперервна функція в будь-якій точці .

2) Дробово-раціональна функція неперервна в усіх точках числової осі, крім тих точок, у яких знаменник дорівнює нулю.

Крім того, слід зазначити, що функції є також неперервними в усіх точках області визначення.

136. Які з функцій, графіки яких зображено на рис. 24, неперервні, а які розривні в точці 0?

Рис. 24

137. Укажіть проміжки неперервності функцій 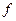і 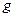, зображених на рис. 25 – 26

Рис. 25 Рис. 26

138. Побудуйте графік функції 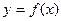. Чи міститься в області визначення функції точка, в якій функція не є неперервна?

1) 2)

139. Чи буде неперервною в будь-якій точці області визначення функція:

1) 2)

3) 4)

● Якщо неперервна функція перетворюється в нуль у точках і і між цими точками інших коренів немає, то в проміжку функція зберігає свій знак.

На цій властивості неперервної функції ґрунтується метод інтервалів розв’язування дробово-раціональних нерівностей.

Для того, щоб розв’язати дробово-раціональну нерівність методом інтервалів треба:

1) Знайти корені чисельника і знаменника дробово-раціональної функції;

2) Нанести корені на числову вісь;

3) Визначити знак дробово-раціональної функції на кожному з утворених інтервалів;

4) Виписати відповідь.

140. Розв’язати нерівності:

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

11) ; 12) ;

13) ; 14) ;

15) ; 16) .

До змiсту