Окружность. Окружность - геометрическое место точек, равноудаленных от центра (рис.5.1)

Окружность - геометрическое место точек, равноудаленных от центра (рис.5.1)

Рис. 5.1.

Эллипс

Эллипс - геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух данных точек F₁ и F₂ той же плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а и большая, чем расстояние между фокусами 2с. Выведем уравнение эллипса, исходя из данного определения. Выберем систему координат как показано на рис 5.2

(Расстояния любой точки M(x,y) эллипса до фокусов называются ее фокальными радиусами. Пусть M(x,y) - произвольная точка эллипса, числа r ₁ и r ₂ –фокальные радиусы т. M:

r ₁ =F₁M; r ₂=F₂M; r₁ +r₁ =2а (см. рис.5.2), тогда r ₁= а - 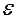х; r₁ = а + 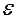х (5.2.1), где , а - большая полуось эллипса, с - половина расстояния между фокусами. Формулы (5.2.1) линейно выражают фокальные радиусы любой точки эллипса через ее абсциссу.)

r ₁ = F₁M = ; r ₂ = F₂M =

F₁M + F₂M = + 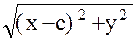= 2а

Это уравнение эллипса приведем к более простому виду: возводя дважды это уравнение в квадрат и преобразуя его, получим:

x² + 2xc + c² + y² = 4a² - 4a 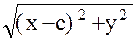+ x² - 2xc² + y²;

xc - a² =-a 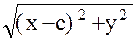; x²c² - 2xca² + a⁴ = a²(x² - 2xc + c²) + a²y;

x²(c² - a²) - a²y² = a²c² - a⁴; x²(a² - c²) + a²y² = a²(a² - c²); x²b² + a²y² = a²b²,

где положили а² - с² = b². Деля обе части последнего равенства на a²b², получим каноническое уравнение эллипса; (5.2.2)

Как видно из этой формулы эллипс симметричен относительно осей OX и OY, т.к. вместе с точкой (x,y) ему принадлежат и точки (-x,-y), (-x, y), (x, -y). Точки пересечения с осями называются вершинами эллипса и равны x = 0; y = b; y = 0; x = a (5.2.3)

Определение: Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.

Обозначив эксцентриситет через 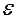, получим (5.2.4)

Эксцентриситет характеризует форму эллипса. Эксцентриситет эллипса содержится в промежутке (0, 1).