Задачи для самостоятельной работы. 3.6.1. Найти угловой коэффициент каждой из прямых, которые заданы уравнениями:

3.6.1. Найти угловой коэффициент каждой из прямых, которые заданы уравнениями:

1. .

2. .

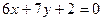3. .

4. .

3.6.2. Написать уравнение прямой, пересекающей ось Ох в точке с ординатой и образующей с осью Ох угол .

3.6.3. Определить острый угол между прямыми и .

3.6.4. Через начало координат провести параллельную и перпендикулярные прямые к данной прямой .

3.6.5. Через точку провести прямую, перпендикулярную к прямой .

3.6.6. Через точку пересечения прямых и провести прямую так, чтобы она прошла, кроме того, и через точку .

3.6.7. Через точку пересечения прямых и провести прямую под углом к первой из них.

Указание. Использовать формулы (3.4.1) и (3.3.1).

3.6.8. Найти уравнение прямой, проходящей через точку и образующей в I четверти с осями координат треугольник, площадь которого равна 16.

Указание. Уравнение прямой находится по формуле:

(3.6.8)

Это уравнение прямой называется уравнением в отрезках.

Вопросы для самопроверки к разделу 3

3.7.1. Какие виды задания прямой на плоскости Вы знаете?

3.7.2. Напишите параметрическое уравнение прямой в векторной и координатной формах.

3.7.3. Найти координаты точки С пересечения медиан треугольника, вершины которого находятся в точках (В механике доказывается, что С является центром тяжести однородного треугольника).

Указание: использовать формулы (3.5.7).

3.7.4. Исходя из уравнения прямой с угловым коэффициентом y=kx+b, при различных значениях параметров k и b записать:

а) уравнение прямой, проходящей через начало координат;

б) уравнение прямой, параллельной оси Ох;

в) уравнение прямой, параллельной оси Оу;

д) уравнение прямой, совпадающей с осью Оу.

3.7.5. Всякое ли алгебраическое уравнение первой степени определяет прямую линию? Запишите общее уравнение прямой.

3.7.6. Пусть дано общее уравнение прямой: Ах+Ву+С=0

Привести это уравнение к уравнению с угловым коэффициентом.

3.7.7. Написать уравнение прямой, проходящей через заданные точки . Какая связь между уравнением прямой, проходящей через две точки, и каноническим уравнением прямой, проходящей через эти точки.

3.7.8. Выведите условие, при котором три данные точки лежат на одной прямой.

3.7.9. Пусть даны прямые и 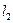. Дайте определение угла между двумя пересекающимися прямыми. Условия параллельности и перпендикулярности двух прямых

3.7.10. Записать формулы нахождения угла между двумя прямыми, если прямые заданы уравнениями:

1) ;

2)

3)

3.7.11. Определить расстояние между двумя параллельными прямым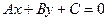и

и .

Ответы к 3.6

3.6.1.

3.6.2.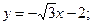

3.6.3.

3.6.4. и ;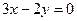

3.6.5.

3.6.6.

3.6.7.

3.6.8. и ;

3.6.9.

Ответы к 3.7

3.7.3.

3.7.4. а) при b=0 => y=kx;

б) при k=0 => y=b;

в) при k=b=0 => y=0;

г) x=a;

д) x=0;

3.7.7. - есть направляющий вектор прямой, который либо параллелен прямой, либо принадлежит ей.

3.7.8.

3.7.10. 3)

3.7.11. Указание. Найти абсциссу точки пересечения второй прямой с осью Ox и использовать формулу (3.3.3). Ответ:

4. Преобразование координат
на плоскости

Одни и те же линии в разных системах координат имеют разные по сложности уравнения. Поэтому, чтобы лучше представить себе линию или фигуру, прибегают к замене систем координат.