Решение типовых задач к разделу 3

3.5.1. Найти уравнение окружности радиуса R с центром в точке C(a,b)

Решение. По определению окружности расстояние любой точки M(x,y), лежащей на окружности, от ее центра C(a,b) равно длине радиуса R, т.е. CM=R.

Найдем длину отрезка CM и выразим равенство CM=R с помощью текущих координат точки M:

3.5.2. Найти точки пересечения линий 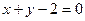и

Решение. Система уравнений

имеет два решения: и 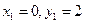, следовательно, данные линии имеют две общие точки и .

3.5.3. Составить уравнение прямой линии, образующей с осью Ох угол 60° и пересекающей ось Оу в точке (0,-2). Выяснить, проходит ли эта прямая через точки А(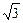,1) и В (2,5)

Решение. Из условия задачи следует, что начальная ордината b=-2, угловой коэффициент , следовательно, по формуле (3.1.7) имеем .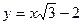

Подставляя в искомое уравнение прямой координаты точки А вместо текущих координат, получим 1=3-2, т.е. 1=1.

Прямая проходит через точку А(,1).

Аналогично, подставляя в уравнение координаты точки B, получим: .

Прямая не проходит через точку В.

3.5.4. Уравнение привести к уравнению с угловым коэффициентом

Решение. Данное уравнение решим относительно 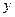, получим уравнение .

Отсюда видно, что , .

3.5.5. Написать уравнение прямой, проходящей через данные точки
А(2,-5) и В(1,3)

Решение. Используя формулу (3.8) запишем уравнение данной прямой

3.5.6. Написать уравнение прямой проходящей через точку

1. Параллельно вектору .

2. Перпендикулярно вектору .

Решение.

1. Используя каноническое уравнение прямой (3.5), имеем или .

2. Используем уравнение (4.1): . Имеем или .

3.5.7. Найти координаты M(x,y,z), делящей отрезок M₁M₂ в отношении , если M₁(1,2,3), M₂(3,9,-2)

Решение. Используем формулы деления отрезка в заданном отношении .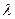

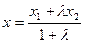, , , , , (3.5.7)

3.5.8. Найти угол между прямыми и

Решение. По формуле (3.3.1) получим , где , , .

Здесь угол отсчитывается от прямой .

3.5.9. Выбрать значение коэффициента 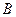прямой

таким, чтобы эта прямая была:

1. Параллельна прямой .

2. Перпендикулярна прямой .

Решение.

1. Используя условие параллельности прямых, получим
, .

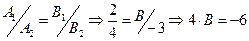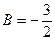2. Используя условие перпендикулярности прямых, получим

, .

3.5.10. Найти уравнение прямой, проходящей через точку пересечения прямых и , а также:
а). точку , б). перпендикулярно прямой

Решение.

a) Используем уравнение пучка прямых, проходящих через точку пересечения данных прямых . Имеем . Число 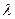найдем из условия, что прямая должна проходить через точку : Подставляя найденное значение в уравнение пучка, получим

.

b) Используя условия перпендикулярности прямых, можем записать . Подставляя в уравнение пучка, получим .