Общее уравнение прямой на плоскости. Положение прямой на плоскости однозначно определяется заданием точки на прямой и вектором, перпендикулярным (нормальным) к ней (рис

Положение прямой на плоскости однозначно определяется заданием точки на прямой и вектором, перпендикулярным (нормальным) к ней (рис. 3.2).

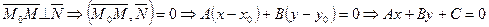(3.2.1)

где , ,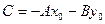

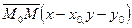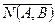
Уравнение Ах+Ву+С=0 называется общим уравнением прямой. Желательно запомнить, что вектор 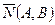, проекции которого на оси координат равны соответствующим коэффициентам при x и у, является перпендикулярным (нормальным) к прямой.

3.3. Основные задачи на прямую на плоскости

1. Углом между двумя прямым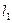и и 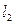называется угол, на который нужно повернуть первую прямую 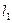до совмещения со второй. Этот угол положительный, если поворот происходит против часовой стрелки, и отрицательный - если по часовой (рис.3.3).

Рис. 3.3

Из рис. 3.3 видно, что 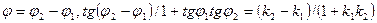, есл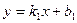и и .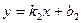

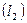Итак, получим формулу:

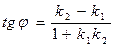(3.3.1)

Условие параллельности прямых 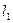и 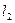: , т.е. угловые коэффициенты равны.

Условие перпендикулярности прямых 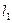и :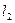

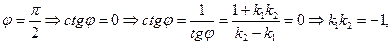т.е. произведение угловых коэффициентов равно -1.

2. Один из углов между прямыми равен углу между нормалями к ним, а угол между векторами (нормалями) находится из формулы:

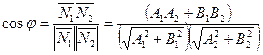, (3.3.2)

где 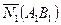и 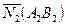нормали к прямым 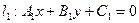и 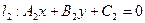. Условие параллельности прямых: 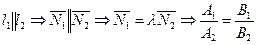, т.е. у параллельных прямых коэффициенты при неизвестных пропорциональны.

Условие перпендикулярности прямых:

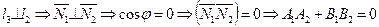
3. Расстояние от точки 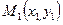до прямой на плоскости равно длине перпендикуляра, опущенного из точки 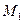на прямую, который в свою очередь равен абсолютной величине проекции вектора 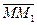на нормаль к прямой, где 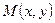- любая точка, лежащая на прямой 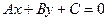. Имеем (рис.3.4)

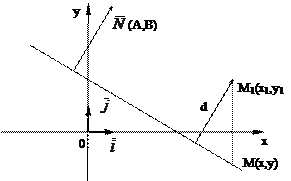
Рис.3.4

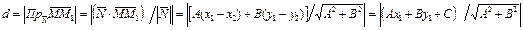(3.3.3)

т.е. расстояние равно абсолютной величине дроби, числителем которой является число, получаемое подстановкой координат точки 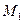в левую часть общего уравнения прямой, а знаменателем - длина нормали к прямой.