Задание математических соотношений

В самом общем виде модель может быть представлена в виде схемы:

Здесь:

X - вектор входных переменных;

Y - вектор выходных переменных;

F - оператор модели, обеспечивающий преобразование входных переменных в выходные в соответствие с задачей, решаемой системой.

Алгоритмы – совокупность операторов, задаваемая с помощью конечной системы правил.

Совокупность правил, образующих алгоритм, должна обладать следующими свойствами:

- полнота: в процессе решения задачи не может возникнуть ситуация, для которой отсутствует указание относительно дальнейших действий;

- однозначность: каждое правило, образующее алгоритм, можно понимать лишь единственным образом;

- непротиворечивость: предписания алгоритму не должны противоречить или взаимоисключать друг друга;

- массовость: возможность использования алгоритма на всем множестве возможных численных значений исходных величин;

- результативность: способность для любых допустимых исходных величин получать результат за конечное число шагов.

Примеры алгоритмов: алгоритмы функционирования (совокупность предписаний, ведущих к выполнению какого либо процесса в системе), алгоритмы управления (совокупность предписаний, определяющих характер воздействия органа управления на исполнительные органы для выполнения ими заданного алгоритма функционирования), алгоритмы контроля, информационно-поисковые и др.

Возможный способ записи алгоритмов - с помощью операторных схем, содержащих пронумерованную последовательность операторов, каждый из которых отображает элементарные операции (группу операций).

Понятие вариационных принципов

Вариационные принципы представляют собой общие утверждения об объекте (системе, явлении) и гласят, что из всех возможных вариантов поведения (движения) выбираются лишь те, которые удовлетворяют определенным условиям. Обычно это достижение экстремального значения некоторой величины при переходе из одного состояния в другое.

Например: законы преломления оптики, движение автомобиля по пересеченной местности – выбирается путь, требующий минимальной затраты времени.

Вариационные принципы уточняются по мере развития человеческих знаний.

В основе вариационных принципов положен анализ соотношения таких философских категорий, как возможность и действительность.

Действительные движения, путь, энергия или другие характеристики материальных систем отличаются от многообразия возможных, но не реализующихся движений – действительные значения могут быть представлены как экстремальные случаи из всех мыслимых.

Классическая механика основывается на законах Ньютона, установленных для свободных материальных точек, и аксиомах связей – справедливость принципов доказывается исходя из этих аксиом. С другой стороны, любой из принципов можно принять за аксиому и из нее логически вывести законы механики.

Дифференциальные уравнения движения, все положения и законы механики могут быть получены как следствие некоторых более общих положений – вариационных принципов механики. Законы сохранения эквивалентны вариационным принципам и поэтому могут рассматриваться как следствие последних.

В качестве основных моделей механики могут рассматриваться не только дифференциальные уравнения, связывающие параметры движения в данный момент, но также некоторые общие свойства, характеризующие движение механической системы в целом на любом произвольном отрезке времени - вариационные принципы, математически выраженные в форме вариационных соотношений из которых как логические следствия вытекают дифференциальные уравнения движения и все положения и законы механики. Построение моделей с помощью вариационных принципов по своей широте и универсальности сопоставим с возможностями, даваемыми фундаментальными законами.

Законы сохранения эквивалентны вариационным принципам и поэтому могут рассматриваться как следствие последних.

Один из вариационных принципов - принцип минимума рассеяния (диссипации) энергии (природа как бы выбирает наиболее экономный способ достижения цели).

Принцип минимума рассеяния (диссипации) энергии – из всех возможных траекторий перевода системы из одного состояния в другое реализуются лишь те, для которых затраты энергии минимальны. Выбирается такая траектория, двигаясь по которой система в максимальной степени поглощает энергию – траектория минимального рассеяния энергии.

Принцип диссипации энергии строго не доказан.

Принцип устойчивости: реализуются лишь устойчивые формы движения (неустойчивые формы если возникают, то быстро разрушаются·).

Принципы устойчивости и диссипации энергии в ряде случаев могут быть противоречить друг другу – иллюстрация закона единства и борьбы противоположностей.

Например, две формы движения жидкости – и ламинарное и турбулентное движения удовлетворяют законам сохранения. Если количество жидкости Q, протекающее через трубу в единицу времени мало, то реализуется устойчивый ламинарный режим. Он более экономичен, затраты энергии минимальны. Если ввести какое-либо возмущение, оно быстро затухнет. При Q > Q_крит ламинарный режим становится неустойчивым – реализуется турбулентный режим, как отвечающий принципу диссипации, которому отдается предпочтение перед принципом устойчивости.

Разнообразию уровней обобщений явлений в каждом конкретном случае исследований соответствуют различные формы и модификации вариационных принципов.

Вариационные принципы механики, характеризующие свойства движения, по форме подразделяются на дифференциальные принципы – характеризуют свойства движения для любого данного момента времени, и интегральные принципы - характеризуют свойства движения на любых конечных промежутках времени.

Модульное построение моделей

Модулем называется группа элементов системы, описываемая только своим входом и выходом. Вместо термина модуль зачастую используются термины "блок", "подсистема" и др.

Синонимы понятия «модуль»: в технике – «узел», «механизм», «блок»; в программировании – «программа», «программный модуль», «логический блок»; в организации – «подразделение».

Разбиение системы на взаимодействующие модули (подсистемы) зависит от цели исследования и может иметь различную основу, в том числе может иметь материальную (вещественную), функциональную, алгоритмическую, информационную и др. основу. Разбиение системы на модули способствует более эффективной организации анализа и синтеза систем, так как оказывается возможным, абстрагируясь от второстепенных деталей, уяснить суть основных соотношений, существующих в системе и определяющих исходы системы.

Примером систем, у которых при разбиение на подсистемы вещественная, функциональная и информационные основы слиты, являются системы управления оргсистемами.

Вместо термина модуль зачастую используются термины "блок", "подсистема" и др.

Модули можно рассматривать как преобразователи потоков (материи, информации, энергии), циркулирующих в рассматриваемом объекте.

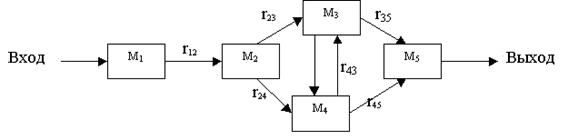
Отношения инцидентности связывают выход одного модуля со входом другого и обеспечивают их согласованность. Для этого бывает достаточно преобразовать данные одного типа в данные другого типа (осуществить перевод с одного "языка" на другой).

Декомпозиция системы на взаимодействующие модули (подсистемы) зависит от цели исследования и может иметь материальную (вещественную), функциональную, алгоритмическую, информационную и др. основу (пример – организационные системы). При этом осуществляется согласование отдельных модулей, их входов и выходов.

Структура полученной сложной модели должна соответствовать структуре и иерархии исходной системы, точнее, полученная модель должна быть адекватной исходной модели в том смысле, как это определено выше для прикладных исследований.

X _ВН – внешние воздействия;

X _Э – воздействия (связи) от других элементов модуля М на систему;

У _ВН - воздействия (связи) от элементов модуля на внешнюю среду (не-систему);

У _Э - воздействия (связи) от элементов системы на другие элементы системы.

Связи X - М можно рассматривать как часть U _j функции U, которая реализуется модулем М.

Разбиение системы на модули способствует более эффективной организации анализа и синтеза систем, так как оказывается возможным, абстрагируясь от второстепенных деталей, уяснить суть основных соотношений, существующих в системе и определяющих исходы системы.

Простейшая модель модуля – модель "черного ящика".

В модели "черного ящика" рассматривается объект, о котором известны только зависимости выходов от входов, - описываются только внешние связи и функции (оклик системы на внешние воздействия). Такая модель не рассматривает внутреннее устройство системы - нет информации о составляющих объект элементах, то есть неизвестны его Х-параметры. Поэтому функция объекта записывается в упрощённом виде, как его реакция на внешние воздействия.

Формальная запись модели «черного ящика» в виде преобразования:

({ X_ВН}, {X_Э}, М) ({У_ВН}, {У_Э}).

Трудность построения математических моделей "черного ящика" состоит в том, чтобы определить, какие реальные связи из бесчисленного множества необходимо включить в модель. Тот факт, что мы не включили в модель остальные связи, не лишает их реальности – они все равно воздействуют на систему независимо от того, включили мы их в рассмотрение, или нет. Критерием включения связи должны служить цели исследования, существенность той или иной связи по отношению к этим целям (неформальная задача).

Исследуя поведение модели "черного ящика", описывающей систему, т.е. изменяя некоторым определенным образом входные воздействия и исследуя влияние этих изменений на выходы, можно достигнуть такого уровня знаний свойств системы, который позволит предсказать изменение ее выходных параметров при любом изменении входных параметров в исследуемом диапазоне.

Однако, как бы детально не изучалось поведение "черного ящика", мы никогда не сможем понять его внутреннее устройство, поскольку одну и ту же реакцию на внешние воздействия могут иметь различные системы с различным внутренним строением. Поэтому изучение системы методом "черного ящика" принципиально не может привести к выводу о ее внутреннем строении, поскольку поведение ее не отличается от поведения изоморфных ей систем.

Этот метод широко применяется в тех случаях, когда представляет интерес поведение системы, а не ее строение (например, при исследовании сложных управляемых систем). Модель "черного ящика" часто оказывается единственно применимой для исследований - исследование живого организма, отсутствие данных о строении системы (исследование электрона).

2.3 Требования к построению модели

Требования к модели определяются исходя из ее основного свойства - модель должна обладать существенными признаками объекта моделирования и быть работоспособной. Работоспособность модели означает возможность ее использования по назначению в соответствующей среде ("исследователь – ЭВМ – окружающая среда"), реализующей необходимые условия функционирования модели.

Принципы и подходы к построению математических моделей

Принципы определяют те общие требования, которым должна удовлетворять правильно построенная модель. Рассмотрим эти принципы.

1.Модель должна строиться исходя из цели исследования системы (явления, процесса) и соответствия цели точности результатов моделирования.

2. Соответствие целям исследования для решения конкретного класса задач, исходя из которых выбираются существенные свойства системы.

Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Строить модель, приближающуюся по сложности к реальной системе не имеет смысла.

3. Абстрагирования от второстепенных деталей - упрощение при сохранении существенных свойств системы. Детализация модели определяется необходимой точностью решения задачи для достижения цели исследования.

Модель должна быть в некоторых отношениях проще прототипа и соответствовать реальной системе по уровню сложности исходя из выбранного множества свойств - игнорируются менее существенные свойства, не оказывающие влияния на решение поставленной задачи, детально рассматриваются основные исследуемые свойства.

4. Блочная структура модели и минимальные связи между блоками с учетом разделения модели по этапам и режимам функционирования системы.

Это дает возможность использования накопленного опыта в процессе отработки модели и многовариантной реализации блоков, отличающихся по точности и сложности, - построения ансамбля моделей.

Адекватность и достоверность модели

Модель адекватна (adaequatus – приравненный) объекту, если результаты моделирования удовлетворяют исследователя по заданной степени точности и могут служить основой для прогнозирования поведения или свойств исследуемого объекта. Адекватность модели зависит от целей моделирования и принятых критериев оценки выполнения целей.

Предпочтительна та модель, которая, позволяя достичь желаемых результатов, является более простой. При этом адекватность и простота не являются противоречивыми требованиями.

Для объекта любой сложности, можно предположить существование множества его моделей, различающихся по степени полноты, адекватности и простоты. Учитывая заложенную при создании неполноту модели, можно утверждать, что идеально адекватная модель принципиально невозможна.

Адекватность - качественное и количественное совпадение именно тех характеристик модели с объектом, которые важны в данном конкретном случае, и в той мере, в которой это достаточно для достижения цели исследования (степень соответствия действительности предсказаний, сделанных на основе модели исходя из целей моделирования).

Оценка адекватности математической модели – определяется степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.

Модель, адекватная при анализе одних характеристик, может быть неадекватна при анализе других.

Вопрос, что является для данной модели существенным, а что нет, решается неформально на основе качественного анализа и с помощью количественных вычислений при проверке модели.

Требование реализуемости модели заставляет сокращать число учитываемых факторов за счет их ранжирования по степени влияния на адекватность модели, что осуществляется при решении каждой конкретной задачи на каждом уровне.

Забвение того, что всякая адекватность математической модели реальному объекту лишь относительна и имеет свои рамки применимости, может привести к грубым ошибкам, основанным на бесконтрольном приписывании реальному объекту свойств его модели.

В сложных случаях мы можем говорить об адекватности лишь с некоторой долей уверенности. Эта уверенность повышается, если следствия из принятой модели хорошо согласуются с надежно установленными фактами или физическим экспериментом.

Довольно часто бывает, что модель, построенная для изучения некоторых свойств объекта, адекватность которой установлена по отношению к этим свойствам, оказывается адекватной и по отношению к каким-то другим свойствам.

Говоря о математической модели и ее адекватности, часто не упоминают о том, какие именно свойства объекта моделируются. При этом нельзя забывать о принципиальной ограниченности области возможного применения любой математической модели.

Качественная адекватность модели (адекватность функционального описания) - соответствие характера реакции системы и модели на изменения входных параметров. Качественная адекватность предполагает оценку совпадения с экспериментальными данными вида функции (убывающая или возрастающая, с одним или несколькими экстремумами).

Понятию качественной адекватности близко понятие достоверности.

Понятию качественной адекватности близко понятие достоверности. Достоверность (полнота) модели: отражение в достаточной мере именно тех характеристик и особенностей моделируемого объекта, которые соответствуют поставленной цели исследования.

Еще одна неформальная, загадочная форма подтверждения достоверности – красота - уверенность, что красиво, то достоверно (красота формы самолета).

Каждая модель содержит условия своей истинности явно, например, в форме допущений и предположений, или неявно, что можно обнаружить, испытывая модель.

Для оценки достоверности необходимо выявить: что известно точно (достоверно), что – с оцениваемой степенью неопределенности (например, с известной вероятностью для стохастических моделей), что можно считать достоверным только при выполнении определенных условий, что известно о том, что неизвестно.

С одной стороны, при создании модели необходимо обеспечить способность модели отображать свойства системы истинно, полно и точно, с другой стороны – обеспечить простоту, умеренную сложность модели для ее приемлемой реализуемости. Эти противоречивые требования решаются неформально - в зависимости от поставленной задачи.

Требование достоверности вынуждает строить модель как можно более полную, точную – учитывать больше факторов на каждом уровне, увеличивать количество уровней иерархии.

С понятием достоверности связано прежде всего понятие упрощенности моделей – приближенностью отображения действительности – различия неизбежны – модель это другой объект (единственной совершенно точной картой местности является сама местность). Различие само по себе не может быть ни большим, ни малым: само по себе оно либо есть, либо его нет. Величину, меру, степень приемлемости различия можно ввести только соотнося его с целью моделирования. Пример: различная точность часов для различных целей.

Количественная адекватность модели - соответствие количественных характеристик тем частным случаям, для которых уже имеются фактические данные или апробированные на практике модели – соответствие выходов модели и объекта при одинаковых условиях с заданной точностью. Количественная адекватность модели (мера адекватности) оценивается в зависимости от заданной точности решения задачи (определяется целью исследований) - осуществляется оценка принятых гипотез и допущений для различных начальных условий. Модель считается адекватной, если она отражает заданные свойства объекта с приемлемой точностью (с относительной погрешностью не более некоторого заданного значения).

Понятия достоверности и адекватности являются условными, поскольку мы не можем рассчитывать на полное соответствие модели реальному объекту, иначе это был бы сам объект, а не модель. Поэтому в процессе моделирования следует учитывать адекватность не модели вообще, а именно тех ее свойств, которые являются существенными с точки зрения проводимого исследования. В процессе проверки модели необходимо установить включение в модель всех существенных факторов. Сложность решения этой проблемы зависит от сложности решаемой задачи.

Адекватность модели может не удовлетворять исследователя по многим причинам: из-за идеализации внешних условий и режимов функционирования; исключения тех или иных параметров; пренебрежения некоторыми случайными факторами. Отсутствие точных сведений о внешних воздействиях, определенных нюансах структуры системы, принятые аппроксимации, интерполяции, предположения и гипотезы также ведут к уменьшению соответствия между моделью и системой. Это приводит к тому, что результаты моделирования будут существенно отличаться от реальных.

Простейшей мерой адекватности может служить отклонение некоторой характеристики оригинала и модели,

или

Тогда можно считать, что модель адекватна с системой, если вероятность того, что отклонение не превышает предельной величины , больше допустимой вероятности :

Практическое использование данного критерия адекватности зачастую невозможно по следующим причинам:

- для проектируемых или модернизируемых систем отсутствует информация о значении характеристики ;

- система оценивается не по одной, а по множеству характеристик, у котолрых может быть разная величина отклонения;

- характеристики могут быть случайными величинами и функциями, а часто и нестационарными;

- отсутствует возможность априорного точного задания предельных отклонений и допустимых вероятностей .

Понятие адекватности включает в себя понятия устойчивости и точности модели.

Устойчивость математической модели - изменение в определенных пределах параметров модели не вызывает качественного изменения ее свойств.

Точность математической модели — ее свойство, отражающее степень совпадения предсказанных с ее помощью значений параметров объекта с истинными значениями этих параметров. Точность модели тесно связана с понятием количественной адекватности.

Истинные значения параметров объекта обычно отождествляют с экспериментами полученными на модели (в том числе в результате вычислительного эксперимента). Однако погрешности эксперимента во многих случаях оказываются соизмеримыми с погрешностями математической модели а иногда и заметно их превышают.

Пусть объект характеризуется n выходными параметрами У = (У ₁, У ₂, … У _i,… У _n). Пусть У _i^м и У _i^р - найденное при помощи матмодели и реальное значения i-го выходного параметра. Точность оценивается относительной погрешностью ε = У _i ^м - У _i ^р / У _i ^р, i = 1, n.

Уточнение модели состоит в том, что в базовый (грубый) вариант модели, добавляются детали, пока модель не достигнет желаемого качества (необходимой точности).

Универсальность – полнота отображения свойств реального объекта, возможность использования модели для группы однотипных объектов и режимов их функционирования.

Увеличение универсальности (расширение группы объектов, для которых может использоваться модель) значительно усложняют модель.

Требования адекватности, экономичности, универсальности противоречат друг другу. Поскольку качество любого объекта проявляется во множестве взаимосвязанных между собой свойств, адекватная модель должна отображать как можно больше свойств.

Стремление во всех случаях обеспечить максимальное внешнее правдоподобие может привести к существенным упрощениям, необходимым для реализации модели. И, наоборот, могут быть разработаны модели, в которых при небольшом внешнем правдоподобии используются весьма точные математические методы.

Равнозначимость внешнего и внутреннего правдоподобия

Внешнее правдоподобие - свойства, которые влияют на результаты решения именно этой задачи. Излишние подробности, не влияющие или слабо влияющие на результаты, должны быть исключены (бритва Оккама): они могут усложнить решение задачи и тем самым ухудшить точность решения. В то же время, не должны быть искажены отношения между элементами системы.

Внутреннее правдоподобие зависит от принятых вычислительных методов и техники, используемой при реализации модели.

Разумная степень равнозначимости внешнего и внутреннего правдоподобия должна быть выбрана в каждом конкретном случае: нет смысла применять сложные вычислительные методы, если необходимые для расчета исходные данные отсутствуют, или они известны с большими погрешностями. Такую модель необходимо заменить другой, пусть менее точной, но опирающейся на доступную достоверную информацию·.

Между качеством входной информации и внутренним правдоподобием должен быть установлен своеобразный уровень равнозначности - нет смысла применять сложные вычислительные методы, если заданная мера адекватности достигается простыми методами или необходимые для расчета исходные данные отсутствуют (либо они известны с большими погрешностями).

Для каждой модели существует область применимости (границы размыты): набор объектов и свойств, которые описываются моделью адекватно. Другими словами – любой объект можно моделировать большим числом моделей, каждая из которых будет адекватна в своих границах применимости.