Пример анализа на чувствительность экономической задачи

Первая задача: на сколько можно сократить или увеличить запасы ресурсов?

После нахождения оптимального решения представляется вполне логичным выяснить, как отразится на оптимальном решении изменение запасов ресурсов. Особенно важно проанализировать следующие два аспекта.

На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции z?

На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?

Вторая задача: увеличение объема какого из ресурсов наиболее выгодно?

Третья задача: в каких пределах допустимо изменение целевой функции?

Каков диапазон изменения целевой функции, при котором не происходит изменения оптимального решения?

Пример анализа чувствительности при анализе эффективности инвестиций.

1 Выбор ключевого показателя эффективности.

2 Выбор факторов, относительно которых разработчик инвестиционного проекта не имеет однозначного суждения (т. е. находится в состоянии неопределенности). Типичными являются следующие факторы:

капитальные затраты и вложения в оборотные средства,

рыночные факторы — цена товара и объем продажи,

компоненты себестоимости продукции,

время строительства и ввода в действие основных средств.

2 Установление номинальных и предельных (нижних и верхних) значений неопределенных факторов, выбранных на втором шаге процедуры. Предельных факторов может быть несколько, например 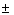5% и 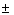10% от номинального значения (всего четыре в данном случае)

3 Расчет ключевого показателя для всех выбранных предельных значений неопределенных факторов.

4 Построение графика чувствительности для всех неопределенных факторов. Ниже приводится пример такого графика для трех факторов.

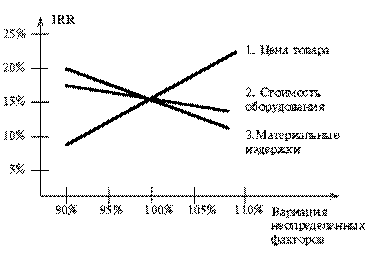
Чувствительность проекта к изменению неопределенных факторов

Данный график позволяет сделать вывод о наиболее критических факторах инвестиционного проекта, с тем чтобы в ходе его реализации обратить на эти факторы особое внимание с целью сократить риск реализации инвестиционного проекта. Так, например, если цена продукции оказалась критическим фактором, то в ходе реализации проекта необходимо улучшить программу маркетинга и (или) повысить качество товаров. Если проект окажется чувствительным к изменению объема производства, то следует уделить больше внимания совершенствованию внутреннего менеджмента предприятия и ввести специальные меры по повышению производительности. Наконец, если критическим оказался фактор материальных издержек, то целесообразно улучшить отношение с поставщиками, заключив долгосрочные контракты, позволяющие, возможно, снизить закупочную цену сырья.

3 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СОСТОЯНИЯ И СТРУКТУРЫ СИСТЕМЫ

3.1 Модель состояния системы

Состояние системы и ее функционирование

Состояние системы - это набор параметров системы, определяющий характер ее функционирования и значение выходной величины на определенном временном интервале.

Состояние системы характеризуется перечнем всех ее свойств и текущими (обычно динамическими) значениями каждого из этих свойств. Перечень свойств системы является, как правило, статическим, поскольку эти свойства составляют неизменяемую ее основу.

Любое происшествие, которое может быть причиной изменения состояния системы, называется событием. Изменение состояний называется переходом.

Если хоть одна характеристика системы изменится, это будет новое состояние. Модель конкретного состояния объекта ("моментальная фотография") – статическая модель. Пример: модель структуры.

Пусть выбран некоторый физический параметр (чаще всего время) такой, что различные состояния соответствуют разным его значениям. Набор состояний - это еще не процесс.

Процесс - набор состояний системы, соответствующий упорядоченному изменению (непрерывному или дискретному) некоторого параметра, определяющего характеристики (свойства) системы - параметра процесса.

Пример: робот-манипулятор. Серия фотографий в разных точках пространства, сделанных наугад или перемешанных – это набор состояний, но еще не процесс. Последовательные во времени движения – процесс.

В системе автоматизированного проектирования процесс проектирования как движение от формулировки задачи к чертежу – основная функция системы.

Функционирование - процессы, которые происходят в системе, стабильно реализующей фиксированную цель. Функционирование системы проявляется в ее переходе из одного состояния в другое или в сохранении какого-либо состояния в течение определенного периода времени.

Кроме основных функциональных свойств компонента, необходимых для выполнения системой целевых задач (свойства первого порядка), компонент привносит с собой в систему нежелательные свойства (свойства второго порядка).

Объект может только менять состояние, вести себя, управляться или становиться в определенное отношение к другим объектам. Иначе говоря, свойства, которые характеризуют объект и его поведение, остаются неизменными.

Например, лифт характеризуется теми неизменными свойствами, что он может двигаться вверх и вниз, оставаясь в пределах шахты. Любая модель должна учитывать эти свойства лифта, так как они входят в его определение.

Функционирование системы проявляется в ее переходе из одного состояния в другое или в сохранении какого-либо состояния в течение определенного периода времени. То есть, поведение системы - это ее функционирование во времени. Пример функционирования: космическая система наблюдения Земли функционирует, наблюдая за заданными объектами с определенной периодичностью.

В реальном мире все без исключения объекты изменяются во времени. Любой объект стремится перейти в некоторое равновесное состояние (принцип устойчивости) как с окружающей средой, так и между отдельными элементами самого объекта. Нарушение этого равновесия приводит к изменениям различных параметров объекта и его переходу в новое равновесное состояние.

Пример параметров этого процесса: изменение во времени линейных, угловых координат, температуры, давления.

Для обоснования принятия решения о наилучшем способе достижения системой заданной цели функционирования необходимо на моделях исследовать различные ситуации, которые могут возникнуть при функционировании системы. Для изучения действий системы разрабатывается модель функционирования (функциональная модель), которая позволит прогнозировать процесс функционирования по заданным начальному состоянию системы и параметрам процесса.

При построении модели функционирования исходя из содержательной постановки задачи определяются:

- основные действия системы, необходимые для выполнения цели (цель действия, описание действия, способ выполнения действия);

- основные компоненты системы, соответствующие действиям;

- основные условия функционирования - интервал времени функционирования, множества входных и выходных воздействий и области их изменения, множества характеристик состояния системы и области их возможных изменений.

В функциональной модели отражены происходящие в системе процессы (физические, химические, механические, информационные и др.), связи параметров системы с внешний средой - описываются свойства системы и ее поведение в пространстве и во времени под влиянием тех или иных воздействий. С помощью нее определяются оптимальные режимы функционирования системы и ее элементов в различных условиях внешней среды и оптимальная организация взаимодействия элементов.

Состояние системы может быть представлено набором из n параметров, каждому состоянию системы соответствует точка в n-мерном пространстве состояний системы, функционирование системы проявляется в перемещении этой точки по некоторой траектории в пространстве состояний (задается начальным состоянием).

Если хоть одна характеристика системы изменится, это будет новое состояние. Модель конкретного состояния объекта ("моментальная фотография") – статическая модель. Пример: модель структуры.

Состояние системы может быть описано ее обобщенными координатами (совокупность параметров, достаточная для определения положения системы) и обобщенными скоростями (производные параметров системы по параметру процесса - времени). Трехмерное представление пространства состояний (фазового пространства) приводится на рисунке.

Состояние системы изображается в виде точки с этими координатами в некотором условном фазовом пространстве. По осям пространства могут лежать любые параметры системы – в общем случае фазовое пространство многомерно.

Фазовые координаты системы - набор численных значений параметров состояния системы.

Для символьной записи процесса изменения состояния системы введем многомерную (по числу исследуемых характеристик) величину z, описывающую их конкретные значения. Все множество возможных величин – Z, z∈Z.

Введем параметр процесса t, множество его значений T, t∈T.

Опишем z как функцию этого параметра z = z (t).

Координаты z₁, z₂,..., z_n – координаты состояния (фазовые координаты). Z (t) – вектор переменных состояния.

Z (t _ф) – вектор состояния (фазовый вектор) в фиксированный момент t = t _ф.

Модель содержит: описание множества возможных состояний и описание закона, в соответствии с которым система переходит из одного состояния в другое.

Тогда процесс S _tot есть некоторое правило перехода от ситуации со значением параметра t_o к ситуации со значением t > t ₀ через все его промежуточные (непрерывные или дискретные) значения:

S _tot (z (t _o)) = z (t), z∈Z, t∈T.

Каждому элементу t множества Т ставится в соответствие вполне определенный элемент z другого множества Z, т.е. в виде отображения z (t) или

T → Z: z (t) ∈Z, t∈T.

Функционирование системы во времени рассматривается как процесс перехода ее из состояния в состояние: состояние системы изменяется как функция времени z (t), называемая фазовой траекторией.

Функции z (t) (или их вероятностные характеристики) могут зависеть от ряда параметров р _m, m = 1, 2,..., m *, р ∈ Р.

В общем случае функции z (t) представляют собой реализации случайных функций Z (t) с совокупностью многомерных законов распределения L [ Z (t)].

Состояние системы может определяться набором действительных чисел. Например, положение самолета в данный момент времени можно описать вектором фазовых координат (z ₁, z ₂, z ₃), где z ₁ – наклонная дальность, z ₂ - азимут, z ₃ - угол места.

В начальный момент времени t₀ состояния z имеют значения, равные z₀ (в общем случае задаются законом распределения L ₀[ Z (t₀)]).

В любой момент времени состояние объекта определяет набор свойств (обычно статический) объекта и текущие (обычно динамические) значения этих свойств. Под "свойствами" подразумевается совокупность всех связей и элементов объекта.

Статическая модель "черного ящика" - свойства системы не изменяются во времени.

При построении статической модели отображаются свойства системы, не зависящие от времени (модели "черного ящика" и структуры системы).

Следующий шаг состоит в том, чтобы конкретнее отобразить происходящие изменения во времени: различаются части, этапы происходящего процесса, рассматриваются их взаимосвязи. Например, динамический вариант "черного ящика" – описание изменения состояния "ящика" во времени (от начального до конечного состояния).

В процессе функционирования может изменяться модель состава: включаются новые элементы в некоторой последовательности действий.

Пример: сетевой график производства – графы сетевой структуры. Вершины графа – выполняемые производственные операции, ребра указывают, какие операции не могут начаться, пока не выполнятся предыдущие. Длительности операций задаются длинами или весами ребер, что позволяет находить на графе "критические пути", т.е. последовательность операций, от которых зависит ритмичность всей работы.

В динамической модели "черного ящика" задаются процессы на входах и выходах. Рассматривая выход у (t) системы (это может быть вектор) как ее реакцию на управляемые u(t) и неуправляемые ν(t) входы x (t) = { u (t), ν (t)}, можно модель "черного ящика" выразить как совокупность двух процессов: X T = { x (t)} и Y T = { у (t)}, t ∈ T.

Если считать у (t) результатом некоторого преобразования Ф процесса x(t) в "черном ящике", т.е. у (t) = Ф (x(t)), то модель "черного ящика" предполагает, что это преобразование неизвестно.

Формализация процесса функционирования системы

Формализация процесса функционирования системы основана на следующих положениях:

- любая система функционирует во времени, взаимодействуя с внешней средой, и в каждый момент времени может находиться в одном из возможных состояний;

- в данный момент времени состояние системы определяется предыдущими состояниями и входами системы, выходные параметры определяются состояниями и входами, относящимися к данному и предшествующим состояниям системы.

Основные составляющие модели: модели отдельных элементов (подсистем) системы, внешние параметры (воздействия окружающей среды или управлений), внутренние параметры (состояние и процессы в моделируемой системе, которые определяют выходные параметры), функциональные соотношения между внешними и внутренними параметрами модели (оператор модели). В динамической модели все составляющие модели имеют временной характер.

Параметры могут быть постоянными или переменными, управляемыми или неуправляемыми. На переменные параметры устанавливаются ограничения - пределы их изменения.

Математическая модель системы - это задание множества входов, состояний, выходов и связей между ними (отображений):

.

Здесь:

Х – входы в систему, x Î X;

Z – состояние системы z (t) = α (t), z ∈ Z;

Y – выходы системы у (t) = β (t, z (t)), t ∈ T;

α – отображение (функция, правило перехода), определяющее зависимость состояния системы от входных воздействий;

β – отображение (функция, правило перехода), определяющее зависимость выходных воздействий от состояния системы.

Конкретизируя множества X, Z и Y и отображения α и β, можно перейти к моделям различных систем.

В обобщенном виде модель характеризуется следующими воздействиями, параметрами и правилами:

x - набор входных воздействий в системе и вся их допустимая совокупность X, x Î X;

у - набор выходных воздействий в системе и вся их допустимая совокупность У, уÎ У;

р - набор постоянных параметров, характеризующих свойства системы и влияющих на выходные воздействия, и вся их допустимая совокупность Р, р Î Р;

z - набор изменяющихся параметров (параметров состояния), характеризующих свойства системы, влияющих на выходные воздействия, и вся их допустимая совокупность Z, z Î Z;

t - параметры процесса в системе и вся их допустимая совокупность T, t Î T;

α - правило (функция, оператор) определения параметров состояния z системы по входам х, постоянным параметрам р, параметру процесса t.

β - правило (функция, оператор) определения выходных характеристик у системы по входам х, постоянным параметрам р, параметру процесса t и параметрам состояния z.

Параметры состояния системы находятся по правилу α из уравнения состояния:

z = α (х, р, t).

Выходные характеристики системы находятся по правилу β из уравнения выхода:

у = β (x, p, t, z).

Входной процесс Х _T - множество значений х (t) входных воздействий, определенных для всех t Î T за весь период функционирования: Х _T { х (t): t Î T }.

Фрагмент входного процесса - отрезок входного процесса, ограниченный моментами времени t0 и t1. Любой входной процесс может быть расчленен на совокупность фрагментов (наоборот – объединение фрагментов - не всегда является входным процессом).

Выходной процесс – выходное воздействие у (t1) на внешнюю среду или другие элементы: У T {у (t): t ∈ T}.

Для всех моментов времени, для которых заданы входные и выходные процессы, определено состояние системы.

Модель функционирования в общем случае для произвольного начального момента времени t ÎT и интервала t₀t₁

z (t₁) = α (t₀t ₁ ,р, z (t₀), Хt₀t₁); у (t₁) = β (t₀t₁,р, z (t₀), Хt₀t₁).

Уравнения состояния и уравнения выхода позволяют описать процесс функционирования системы траекториями Z _Т и У _Т, каждая точка которых характеризует для некоторого момента времени t ∈ T состояние системы z (t). Конкретный вид обеих траекторий определяется входным процессом ХТ, начальным состоянием z (t ₀) и операторами α и β.

На основе введения приведенных воздействий, параметров и правил модель может быть записана как кортеж

∑: {x, у, p, t, z, α, β, β *}, x Î X, у Î У, p Î P, t Î T, z Î Z.

Разбор конкретной модели по такой формализованной схеме состоит в отнесении различных величин, объектов, понятий к составляющим кортежа (составление списков существенных входов, выходов, процессов, параметров), что является эффективным средством понимания функционального содержания системы, составления и корректировки ее модели, выявления важнейших сторон моделирования.