Анализ и синтез в моделировании

Как разделить модель на подмодели, как построить иерархию моделей для исследования элементов (декомпозиция) и как их потом объединить для исследования системы в целом, чтобы объяснить целое через частности – основная проблема моделирования.

В основе общей методологии – сочетание методов анализа и синтеза. Синтез заключается в создании описания объекта, анализ – в определении свойств объекта по его описанию, т.е. при синтезе формируются, а при анализе оцениваются проекты объектов.

Единство анализа и синтеза относится ко всем отраслям знаний, в т.ч. к моделированию. Алгоритмов «анализа – синтеза» как известно, нет – определена только общая методология (как выполняются операции анализа и синтеза).

Анализ

Взаимодействие элементов системы характеризуется прямыми и обратными связями. Сущность анализа системы состоит в том, чтобы выявить эти связи и установить их влияние на поведение всей системы в целом.

Анализ (от гр. analysis - разложение, расчленение) предполагает изучение поведения и свойств системы заданной структуры при взаимодействии с внешней средой (объект существует, необходимо исследовать его свойства - системный анализ, спектральный анализ, анализ крови и т.п.).

Цель исследований – качественная и количественная оценка свойств системы, различных стратегий управления процессами, характеристик элементов и их совокупностей. Основной процедурой анализа является построение обобщенной модели, адекватно отображающей интересующие исследователя свойства реальной системы и ее взаимосвязи. Характеристики процессов определяются как функции параметров системы.

Чтобы разобраться в системе, изучить, исследовать её (задача анализа), надо описать систему, зафиксировать ее свойства, поведение, структуру и параметры, то есть построить одну или несколько моделей.

Для этого надо ответить на три основные вопроса:

- что делает система (узнать поведение, функцию системы);

- как устроена система (выяснить структуру системы);

- каково качество системы (насколько хорошо она выполняет свои функции).

Описание объекта как системы

Между различными видами параметров, существует некоторая зависимость: выходные параметры объекта (а, значит, и его качество), зависят от входных воздействий, параметров внешней среды и от качества составляющих объект элементов (Х -параметров).

Такая зависимость представляется в аналитической форме и называется глобальной (интегративной) функцией объекта.

Существование глобальной функции ещё не означает, что она известна исследователю или проектировщику объекта - необходимо отыскать эту функцию.

Если глобальную функцию не удается представить в аналитической форме, для сложных объектов приводится алгоритмическое описание объекта (в виде поведенческой имитационной модели).

Основная операция анализа (неформальная) – декомпозиция (разделение целого на части). Применительно к построению структуры модели – определение состава модели (компонентов).

Компонент – любая часть предметной области, которая может быть выделена как некоторая самостоятельная сущность. Это и система (модель) в целом, и любая часть системы (модели) – подсистема, элемент.

Основная сложность декомпозиции – определение базовых (неделимых) моделей компонентов, соотношение моделей микро- и макроподхода. В основе декомпозиции – достижение компромисса между полнотой набора формальных моделей рассматриваемой системы и простотой – он может быть достигнут, если в модель включаются только модели компонентов, существенных по отношению к цели моделирования.

Примеры методов анализа - часто применяемые в математике аналитические методы: разложение функций в ряды, спектральный анализ, дифференциальное и интегральной исчисление и др.; в физике – методы молекулярной динамики; на производстве – конвейерная технология изготовления.

Основные положения технологии анализа

В системном анализе одними из наиболее важных критериев эффективности декомпозиции являются критерии полноты декомпозиции и ее простоты, которые прямо связаны с полнотой модели системы, взятой в качестве исходной при декомпозиции и целями ее построения.

Основная операция при анализе – разделение целого на части, т.е. декомпозиция – метод разложения системы на отдельные элементы, который может последовательно выполняться несколько раз.

При декомпозиции должен быть принят некий компромисс межу полнотой и простотой, достигаемый если в структурную модель включаются только элементы, существенные по отношению к цели анализа.

Укрупненный алгоритм декомпозиции

Число уровней декомпозиции (уровней древовидной структуры) определяется следующим образом.

Декомпозиция по каждой из ветвей древовидной структуры ведется до тех пор, пока не приведет к получению элементов системы, не требующих дальнейшего разложения. Такие составляющие называются элементарными.

Для определения элементарности используются как формализованные, так и не формализованные (экспертные) критерии.

Часть системы, которую нельзя считать элементарной на основании выбранных критериев, подлежит дальнейшей декомпозиции. Если исследователь не достиг элементарности на какой-либо ветви древовидной структуры, то вводятся новые элементы в модель, взятую в качестве основания, и декомпозиция продолжается по ним.

Синтез

Процесс синтеза модели на основе системного подхода включает следующие этапы:

1. Формирование требований к модели системы исходя из цели исследований (определяется вопросами, на которые исследователь хочет получить ответы с помощью модели) на основе исходных данных, включающих назначение модели, условия работы системы, внешнюю среду для системы и накладываемые ограничения.

2.Определение подсистем модели исходя из действий системы, необходимых для выполнения назначения системы.

3.Подбор элементов подсистем модели на основе данных для их реализации.

4.Выбор составляющих элементов будущей модели.

Получившаяся таким образом модель является интегрированным целым.

Синтез предполагает создание структуры и характеристик системы, обеспечивающих заданные ей свойства.

Синтез системы включает:

- определение всех необходимых функций, позволяющих решить поставленную задачу;

- нахождение способов выполнения каждой функции (формирование подсистем);

- определение такой схемы взаимодействия подсистем, которая позволила бы выполнить поставленные задачи наилучшим образом.

Составленные в результате синтеза альтернативные варианты структурно-функциональных схем исследуются в процессе анализа – исследуются свойства предварительно разработанных вариантов проекта и эффективность каждого варианта.

Выходные параметры объекта (а, значит, и его качество), зависят от входных воздействий, параметров внешней среды и от качества составляющих объект элементов.

Основные положения технологии синтеза

Многообразие сфер применения сложных систем, возможных структур и стратегий управления процессами порождает огромное множество вариантов их построения, что приводит к невозможности решения задачи синтеза в общей постановке.

•Полученная в результате декомпозиции (анализа) совокупность элементов кроме внешней целостности (т.е. определенной обособленности от окружающей среды, хорошо описываемой моделью «черного ящика») должна обладать внутренней целостностью.

•Внутренняя целостность связана с моделью структуры системы, т.е. установлением отношений между элементами, выполнение которой называется операцией агрегирования – объединение нескольких элементов в единое целое. Результатом агрегирования (синтеза) является система, называемая агрегатом.

•Свойства компонента не являются только совокупностью свойств его отдельных элементов. Компонент может обладать такими свойствами, которых нет ни одного из его элементов, взятых в отдельности, т.е. у компонента появляется новое качество, которое не могло появиться без этого объединения.

Примеры сложных систем

Космическая система наблюдения Земли как сложная техническая система

Задачи космической системы наблюдения Земли

Сейчас обостряются проблемы общемирового масштаба: сокращение запасов критически важных природных ресурсов, нарастание загрязнения и деградация среды обитания, увеличение количества природных и техногенных катастроф, глобальное потепление клиимата, рост терроризма и наркоторговли. Информационное обеспечение этих проблем – на основе оперативного сбора, обработки и предоставления пользователям необходимой информации - предоставляется космической системой глобального мониторинга Земли.

Сегодня в мире насчитывается десятки стран, участвующих в реализации программ космических наблюдений - уровень информатизации становится все более важным критерием оценки могущества и безопасности любого государства и важным средством выработки внутренней и внешней стратегии.

Современные задачи, решаемые космической системой наблюдения Земли:

- метеонаблюдения и анализ изменения климата на планете;

- поиск полезных ископаемых, нефтяных и газовых месторождений;

- анализ крупномасштабной динамики растительного покрова;

- мониторинг водных биологических ресурсов, наблюдение и контроль за деятельностью промысловых судов;

- анализ ледовой обстановки;

- контроль технического состояния промышленных комплексов;

- учет и мониторинг застройки города (контроль над земельными ресурсами и недвижимостью);

- оперативный прогноз и контроль чрезвычайных ситуаций природного и техногенного характера (мониторинг предвестников землетрясений, экологический обстановки, лесных пожаров).

Эти задачи определяют требования к средствам спутникового наблюдения: оперативное наблюдение, повышение разрешающей способности изображений, увеличение полосы съемки, освоение всех информативных диапазонов спектра электромагнитных излучений.

Основные современные тенденции развития спутникового наблюдения – переход на цифровые данные представления пространственной информации, а также на цифровые базы пространственных данных как основы для аналитической работы, связанной с моделированием объектов или процессов.

Возрастает важность военного аспекта – все больше стран хотят иметь цифровые карты все большей разрешающей способности (решение задач разведки и целеуказаний) и постоянно их обновлять.

Пространственные данные, привязанные к местности с помощью современных навигационных систем, выступают как основа для различной информации, и процесс ее обновления бесконечен.

Совместная европейская и американская система спутниковой навигации (Galileo и GPS) даст возможность определять координаты с точностью до 2-3 м в обычном режиме и до миллиметров в дифференциальном - с помощью дифференциальной станции(точно привязанный к местности приемник навигационных сигналов, который на определенной территории выдает поправку другим приемникам спутниковой навигации).

Появились новые возможности - малые приемные станции и программные продукты, которые позволяют в режиме реального времени самостоятельно принимать сырые данные съемки и сразу их обрабатывать (что намного дешевле, чем приобретать обработанные снимки). Это особенно важно для некоторых оперативных задач, например при чрезвычайных ситуациях, при экологическом мониторинге или оперативном мониторинге производства (контроль технического состояния).

Большое развитие получают малые КА (массой до 150 кг), на основе которых в перспективе могут быть сформированы самостоятельные экономически эффективные многоспутниковые системы для сверхоперативного глобального наблюдения за наиболее быстро развивающимися природными и техногенными чрезвычайными ситуациями. Орбитальные системы на основе малых КА смогут обеспечить сочетание высоких характеристик информации с высокой оперативностью. Это стимулирует рост спроса на космическую информацию, что обеспечит высокий инвестиционный потенциал подобных проектов.

Система наблюдения Земли представляет собой сложную многофункциональную техническую систему - совокупность большого числа разнотипных элементов и разнородных связей между ними, объединенных для выполнения комплексных задач.

Система имеет цель, взаимосвязанные составные части образуют многоуровневую структуру и выполняют функции, направленные на достижение цели, имеет управление, благодаря которому все компоненты функционируют согласованно и целенаправленно.

Состав и структура космической системы наблюдения Земли

Космическая система наблюдения Земли может являться частью более обширной системы исследования природных ресурсов (в зависимости от задач системы), включающей космические, авиационные наземные, морские системы наблюдения.

Выделение конкретной системы из внешней среды является субъективным фактором и определяется целями проектирования.

Качество решения задач определяется параметрами системы и характеристиками входящих в космическую систему компонентов.

Космическая система наблюдения Земли – это совокупность функционально взаимосвязанных космических аппаратов и наземных технических средств, предназначенных для решения целевых задач. Структура системы представлена на рисунке 1.1, информационные потоки – на рисунке 1.2.

Основной функциональный элемент космической системы наблюдения Земли – космический аппарат (КА).

Космический аппарат как сложная техническая система имеет цель функционирования (наблюдение Земли и передача на Землю информации о результатах наблюдения), состоит из взаимосвязанных элементов, обеспечивающих выполнение цели системы, является элементом системы более высокого уровня (космической системы наблюдения Земли).

Внешней средой КА являются природное окружение (космическое пространство) и другие компоненты системы наблюдения Земли.

Структурно космический аппарат состоит из двух основных подсистем - полезной нагрузки – целевой аппаратуры (аппаратное и программное обеспечение, необходимые для получения требуемой информации) и платформы, обеспечивающей функционирование полезной нагрузки и передачу полученной информации на Землю (обслуживающая подсистема).

Полезная нагрузка КА

Состав целевой аппаратуры определяется задачами, возлагаемыми на космическую систему наблюдения Земли, и характеристиками объекта наблюдения (внешней средой).

Для получения данных о различных природно-хозяйственных объектах используются как пассивные (фотографические, оптико-механические и оптико-электронные, радиометрические, спектрометрические), так и активные (радиолокационные) системы в ультрафиолетовой (УФ), видимой (В), инфракрасной (ИК) и микроволновой (СВЧ, т.е. сверхвысокочастотной) областях спектра.

Платформа КА обеспечивает условия нормального функционирования полезной нагрузки: поддержание заданных параметров орбиты и ориентации КА, обеспечение требуемых условий функционирования аппаратуры (электропитание, тепловой режим), выдачу полезной нагрузке команд управления, сбор целевой и телеметрической информации и передача ее на Землю, обеспечение конструктивной целостности и жесткости.

Основные подсистемы платформы:

- система управления;

- система ориентации и стабилизации;

- система электроснабжения;

- командно-измерительная система;

- аппаратура спутниковой навигации;

- система ориентации солнечных батарей;

- корректирующая двигательная установка;

- конструкция (включая бортовую кабельную сеть, антенны, систему отделения и терморегулирования).

Общие требования к конструкции:

- минимальный собственный вес;

- обеспечение требуемых углов обзора датчиков информационной аппаратуры и системы ориентации;

- система раскрытия панелей солнечной батареи должна отвечать требованиям безопасности и надежности, а компоновка этих панелей – обеспечивать минимально возможный момент инерции на валу привода СОСБ для снижения массы и энергопотребления последнего;

- обеспечение минимальных возмущающих моментов от светового и аэродинамического давления;

- конструкция должна обеспечивать удобство проведения монтажных, испытательных и отладочных наземных работ, не затрудняя доступ к приборам и кабельной сети;

- при размещении аппаратуры должно быть учтено условие минимизации протяженности кабельных связей для сокращения энергопотерь в проводах и обеспечения электромагнитной совместимости аппаратуры.

Наземная система (наземный сегмент) обеспечивает слежение за КА и управление ним, передачу команд приема и обработки информации полезной нагрузки и телеметрической информации, выдачу информации потребителям. Типовые компоненты наземного сегмента: комплекс управления, комплекс приема, обработки и распространения информации, центр планирования съемок, их архивации.

Если в состав системы наблюдения входит не один космический аппарат, то их совокупность образуют отдельную подсистему – орбитальную группировку. КА в этом случае создается на базе унифицированной космической платформы.

В состав космической системы наблюдения Земли могут входить и ракетно-космические комплексы для создания и поддержания орбитальной группировки системы.

Рисунок 1 Структура космической системы наблюдения Земли

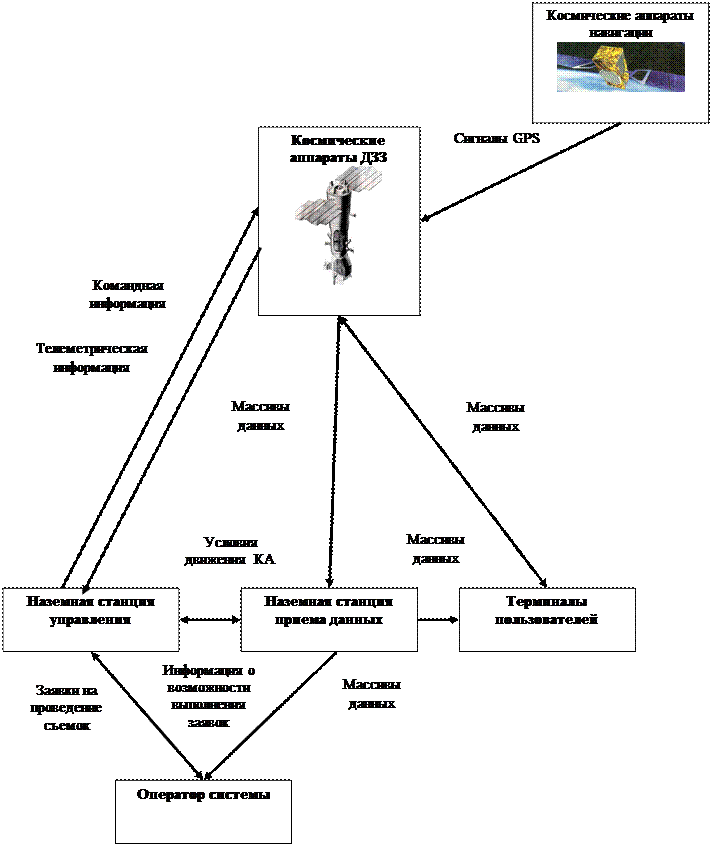
Рисунок 2 Информационные потоки космической системы наблюдения Земли

Космическая система есть единый сложный многокомпонентный многофункциональный распределенный в практически неограниченном по объему трехмерном пространстве. Отдельные компоненты космических систем могут одновременно являться компонентами других систем.

Как кибернетическая система космическая система обладает следующими специфическими чертами:

Является распределенной;

обладает высокой степенью автоматизации, имеет высокий удельный вес информационной составляющей, техническое и технологическое разнообразие;

обладает высокой устойчивостью функционирования;

подсистемы функционируют в условиях неопределенности относительно внешней среды;

является перманентно развивающейся системой;

носит ярко выраженный инновационный характер.

С точки зрения теории систем орбитальная группировка является именно системой, а не просто совокупностью КА: задачи КА и орбитальной группировки принципиально различны. Один КА не способен обеспечить выполнение целевой задачи - выполнение целевой задачи космической системой может быть достигнуто только в результате совокупного функционирования КА.

Расположение элементов в пространстве не является случайным, задачи между КА строго распределены, функционирование отдельного КА в данный момент времени зависит от функционирования остальных КА и состояния всей системы, целевая информация от каждого отдельного КА включается в общий поток.

КА в орбитальной группировке находятся друг с другом в различных отношениях: по расположению в пространстве, по функциональным задачам и др. Орбитальная группировка представляет собой распределенный в пространстве искусственный многокомпонентный космический объект. Этот объект выполняет роль большой космической станции в космической системе.
Сложная социально-экономическая система.

Под экономической системой понимается любая система, в которой действуют стоимостные или натуральные товарные переменные.

В качестве экономической системы может выступать отдельная фирма; техническая или технологическая система, учитывающая стоимость технических средств или продукции; отрасль промышленности; экономика государства.

Экономическая система, в которой действуют социальные факторы, называется социально-экономической. В частности, любая макроэкономическая система государства или региона не может не включать социальный сектор и поэтому является социально-экономической¹.

Международный стандарт ИСО 9000:2000 определяет организацию как группу работников и необходимых средств с распределением ответственности, полномочий и взаимоотношений.

Можно дать и другое определение: организация - это систематизированное, сознательное объединение действий людей, преследующих достижение конкретных целей.

Понятие «организация» раскрывает приведенная на рис. 1 модель технических терминов.

Рис. 1. Виды организаций, представленные с помощью модели технических терминов

Рис. 2. Связи системы-организации с внешней средой.

Создаваемая модель должна давать ответ на следующие вопросы:

• Кто из сотрудников организации должен выполнять конкретные функции?

• При каких условиях нужно выполнять функцию?

• Что должен сделать сотрудник в рамках данной функции?

• Каким образом следует ее выполнять?

• Какие ресурсы при этом необходимы?

• Каковы результаты выполнения функции?

• Какие информационные средства нужны?

• Каким образом все это согласовать?

• Как все это можно осуществить наиболее эффективно?

• Как можно изменить или построить бизнес-процесс?

• Как снизить риск и повысить эффективность изменений?

2 ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

2.1 Математическая модель, математическое моделирование – основные понятия, термины и определения

Математика – наука, изучающая схемы моделей безотносительно к их конкретному воплощению и методы (способы) использования моделей для решения конкретных задач. Требования обеспечения математической строгости в системных исследованиях нереальны (претензии на абсолютную истину), основа системных исследований – неформальное упрощение задачи, адекватное поставленным целям.

Никакое определение не может в полном объеме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

Желательно найти такое определение математической модели, которое давало бы возможность классифицировать (охватывать) все существующие и вновь создаваемые модели. Остановимся на формулировке математической модели, которая отражает ее целевую сущность исходя из понятия математического моделирования как процесса построения модели и исследований с ее помощью.

Термин «математическое моделирование» охватывает методологически малосвязанные разработку модели и ее использование. Иногда моделированием называется каждый из этих двух этапов в отдельности.

Математическое моделирование - это способ исследования различных процессов путем изучения явлений, имеющих различное физическое содержание, но описываемых одинаковыми математическими соотношениями.

Один из аспектов математического моделирования как способа познания - изучение системы, явления с помощью вычислительного эксперимента (в таком понимании термин "вычислительный эксперимент" может быть синонимом термина "математическое моделирование").

Многие задачи исследования систем трудно достаточно хорошо формализовать и свести к математическим моделям, позволяющим ставить и решать поставленные задачи. Непонимание (или неумение четко поставить задачу) часто приводит к «победе математики над разумом». Системный исследователь должен уметь формализовать в математических терминах конкретную задачу исследований - разработать математическую модель.

Практически математическое моделирование как метод исследований не имеет ограничений, так как:

- моделирующая система может одновременно содержать описания элементов непрерывного и дискретного действия,

- быть подверженной влиянию многочисленных случайных факторов сложной природы;

- допустимо описание системы соотношения большой размерности; обеспечивается простота перехода от одной задачи к другой введением переменных параметров, возмущений и различных начальных условий.

Математическая модель как средство познания, исследования реального мира формируется на основании общей методологии системных исследований.

Среди многих подходов к построению систем можно выделить два основных (подходы «снизу» и «сверху») – стремление изучить реально существующие системы и на основании этого сделать выводы о наблюдаемых закономерностях (подход Л. Берталанфи), и рассматривать множество всех мыслимых систем, сокращая его до рациональных пределов (подход У. Эшби).

Математическое моделирование как один из видов знакового моделирования представляет собой формальное описание объекта на языке математики, и исследование модели с помощью математических методов.

Математическое моделирование - процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта.

Математические модели относятся к знаковым моделям.

Математическая модель – описание в виде математических соотношений (например, формул, уравнений, неравенств, логических условий, операторов) состояния, изменения, протекания процессов в системе или явлении (в том числе функционирования системы), в зависимости от параметров системы, входных сигналов, начальных условий и времени.

Математическая модель — это „эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям.

Математическая модель - абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия. (Определение основано на идеализации «вход — выход — состояние», заимствованной из теории автоматов).

Наконец, наиболее лаконичное определение математической модели: уравнение, выражающее идею.

Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, требуемой достоверности и точности решения этой задачи. Математическая модель отражает именно те особенности, которые необходимо исследовать для решения поставленной задачи.

Обычно математическая модель только приближенно описывает поведение реальной системы, являясь ее абстракцией, так как знания о реальной системе никогда не бывают абсолютными, а гипотезы часто вынужденно или намеренно не учитывают некоторые факторы.

Для поддержки математического моделирования разработаны компьютерные системы моделирования, например, Matlab, Matcad и др. Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

Основное качество математических моделей - " вариантность ". Одним знаковым описанием кодируются физически различные системы, явления. На одной и той же модели могут быть изучены большое число вариантов её поведения (путем изменения параметров).

Универсальность моделей: принципиально разные реальные явления могут описываться одной и той же математической моделью. Например, колебательные процессы, имеющие совершенно разную природу описываются одинаковой математической моделью - мы изучаем сразу целый класс описываемых ею явлений.

Основная задача математического моделирования: по заданным входным параметрам найти значения выходных параметров системы (отобразить некоторое заданное множество X значений входных параметров x на множество Y значений выходных параметров y).

Модель — закономерность, преобразующая входные значения в выходные: Y = M (X). Под этим можно понимать таблицу, график, выражение из формул, закон (уравнение) и т. д. Это вопрос способа записи закономерности. Y - некоторый интересующий исследователя показатель.

На этом основании при определении понятия "математическая модель" используется широкое понятие оператора – функция, алгоритм, совокупность правил, обеспечивающие установление выходных параметров по заданным входным параметрам.

Математическую модель можно рассматривать как некоторый математический оператор и сформулировать понятие математической модели следующим образом.

Математическая модель – любой оператор (правило) А, позволяющий по значениям входных параметров x установить соответствующие выходные значения параметров y системы:

А: x → y, x Î X, y Î Y.

Такое широкое определение включает в себя не только все многообразие математических моделей, но и информационные модели – процедуру поиска данных в базе данных можно представить в виде некоторого оператора. В таком контексте информационная модель – специфическая форма математической модели.

Основные понятия в моделировании систем определяются из соответствия аналогичным понятиям системы: элемент системы, связь, внешняя среда.

Моделирование как метод исследования имеет следующую структуру: постановка задачи, создание модели, исследование модели, перенос знания с модели на оригинал.

Математика – наука, изучающая схемы моделей безотносительно к их конкретному воплощению и методы (способы) использования моделей для решения конкретных задач. Требования обеспечения математической строгости в системных исследованиях нереальны (претензии на абсолютную истину), основа системных исследований – неформальное упрощение задачи, адекватное поставленным целям.

Из этого следует множественность моделей одного объекта: для каждой цели требуется своя модель одного и того же объекта (множественность моделей одного объекта, пример – модели самолета для исследований аэродинамики, прочности).

Модель может быть сосредоточена на функциях системы (функциональная модель) или на ее объектах (модели данных).

Функциональные модели выделяют события в системе, представляют с требуемой степенью детализации систему функций, которые в свою очередь отражают свои взаимоотношения через объекты системы.

Модели данных выделяют объекты системы, которые связывают функции между собой и с их окружением и представляют собой подробное описание объектов системы, связанных системными функциями.